Дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:
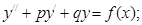
если в правой части уравнения стоит ноль, то
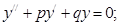
то уравнение называется однородным линейным.
Для решения такого уравнения составляется характеристическое уравнение. Характеристическимназывается квадратное уравнение, полученное на основе дифференциального уравнения, в котором  заменяются новой переменной k, степень которой определяется порядком производной:
заменяются новой переменной k, степень которой определяется порядком производной:
 ;
;
Тогда 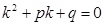 - характеристическое уравнение.
- характеристическое уравнение.
Находим корни характеристического уравнения:

1. Если корни характеристического уравнения действительные и равные  , т.е. дескременант Д=0, то решением дифференциального уравнения будет являться функция:
, т.е. дескременант Д=0, то решением дифференциального уравнения будет являться функция:
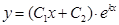 . (1)
. (1)
2. Если корни характеристического уравнения действительные и равные числа  , Д>0, то:
, Д>0, то:
 . (2)
. (2)
3. Если корни характеристического уравнения – комплексные числа при Д<0, т.е. 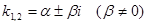 , то
, то
 . (3)
. (3)
Например: Найти общее решение дифференциального уравнения:
1. 
Составляем характеристическое уравнение:
 ;
;
Находим его корни:
 ;
;
k1=k2=k=1
Подставляем полученное значение к=1 равенство (1), получаем:
 .
.
2. 
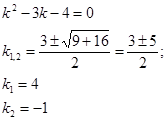
Полученные значения к1 и к2 подставляем в равенство (2), получаем:
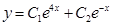
3. 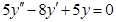
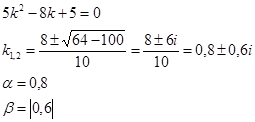
Полученные значения α и β подставляем в равенство (3), получаем:

5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Пусть у нас есть дифференциальное уравнение, разрешенное относительно второй производной:
 ,
,
Рассмотрим виды дифференциальных уравнений второго порядка, которые допускают понижение порядка:
I. Дифференциальные уравнения не содержащие аргумента:
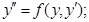 (*)
(*)
Вводим новую переменную Р:
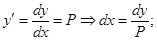
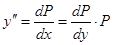 подставляем это в (*) получаем:
подставляем это в (*) получаем:
 .
.
Получили дифференциальные уравнения первого порядка и его решением будет функция:  или
или
 Разделяем переменные, умножая обе части на
Разделяем переменные, умножая обе части на 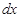 :
:

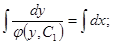
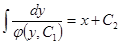 - Общее решение
- Общее решение
Пример:
 .
.
Вводим замену: 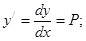 (1)
(1)
Из равенства (1) получаем: 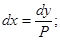 (2)
(2)
Тогда 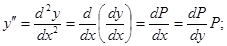 (3)
(3)
Подставляем значения  и
и 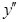 из равенств (1) и (3) в заданное уравнение и получаем:
из равенств (1) и (3) в заданное уравнение и получаем:
 .
.
Получили уравнение первого порядка. Решаем методом разделения переменными Р и у. Уравнение решается относительно Р.
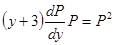 .
.
Сокращаем обе части на Р
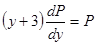 .
.
Делим переменные, умножая обе части на  получаем:
получаем:
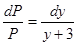 .
.
Интегрируем оба части:
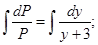

Потенцируем:
 (4)
(4)
Подставляем полученное значение Р из равенства (4) в равенство (1), получаем:
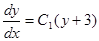
Вновь получили дифференциальное уравнение первого порядка относительно переменных у и х.
Делим переменные, умножая обе части равенства на 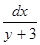 , получаем:
, получаем:

Интегрируем:
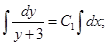
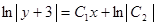 .
.
Потенцируем:
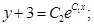
Получаем общее решение дифференциального уравнения:

II. Дифференциальные уравнения не содержащие искомой функции:
 (**)
(**)
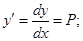

Тогда уравнение (**) примет вид:
 .
.
Решением этого уравнения будет функция: 


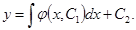 - Общее решение
- Общее решение
Пример:
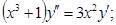
Вводим замену:  (1)
(1)
Тогда 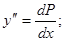 (2)
(2)
Подставляем значения  и
и 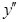 из равенств (1) и (2) в исходное уравнение и получаем:
из равенств (1) и (2) в исходное уравнение и получаем:
 .
.
Делим переменные, умножая обе части на  получаем:
получаем:
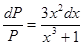 .
.
Интегрируем оба части равенства:
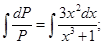
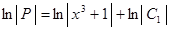
Потенцируем:
 (3)
(3)
Подставляем значение Р из равенства (3) в равенство (1) и получаем:
 .
.
Делим переменные, умножая обе части равенства на 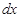 , и интегрируем:
, и интегрируем:
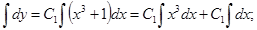
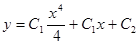 - Общее решение
- Общее решение
III. Дифференциальные уравнения не содержащее искомой функции и её производной:
 (***)
(***)
Подстановка: 
 подставляем в (***)
подставляем в (***)



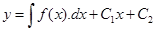 - Общее решение
- Общее решение
Например: Найти общее решение дифференциального уравнения:
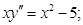
Вводим подстановку:  (1)
(1)
Тогда 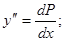 (2)
(2)
Подставляем значения 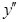 из равенства (2) в исходное уравнение:
из равенства (2) в исходное уравнение:
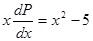 .
.
Делим переменные, умножая обе части равенства на 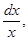 получаем:
получаем:
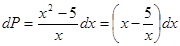 .
.
Решаем полученное уравнение, интегрируя обе части:
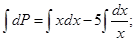
и получаем;
 (3)
(3)
Подставляем значение Р из равенства (3) в равенство (1), получаем:
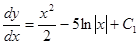 .
.
Делим переменные, умножая обе части равенства на 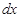 , и интегрируем:
, и интегрируем:
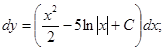
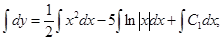
 .
.
Таким образом,
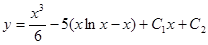 - Общее решение
- Общее решение
Примечание. Решаем интеграл 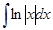 методом интегрирования по частям:
методом интегрирования по частям:

ПРАКТИЧЕСКАЯ ЧАСТЬ
