Тік бұрышты облыс жағдайында қос интегралды қайталанған интегралға келтіру.
ПӘНДЕРДІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕНІ
«Математикалық талдау 2»
B010900-Математика мамандығы үшін
ОҚУ -ӘДІСТЕМЕЛІК МАТЕРИАЛДАР
Семей
МАЗМҰНЫ
1 Глоссарийлар…………..…………………………………………………….3
2 Дәріс оқулар …………………………………………………………………7
3 Практикалық сабақтар........…………………………………………………31
4 Студенттің өздік жумысы...................………………………………………45
ГЛОССАРИЙ
| № | Жаңа ұғымдар | Мазмұны |
| Анықталмаған интеграл | Негізгі интегралдың таблицасы. 1. 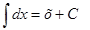 2. 2. 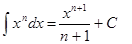 3. 3. 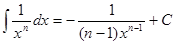 4. 4. 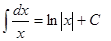 5. 5. 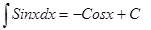 6. 6. 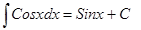 7. 7. 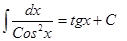 8. 8. 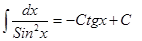 9. 9. 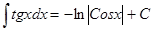 10. 10. 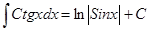 11. 11. 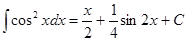 12. 12. 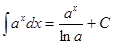 13. 13. 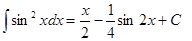 14. 14. 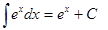 15. 15. 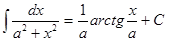 16. 16. 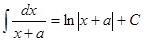 17. 17. 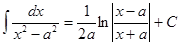 18. 18. 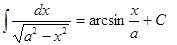 19. 19. 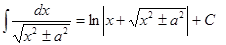 20. 20. 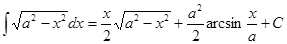 21. 21. 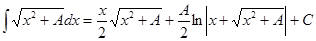 22. 22. 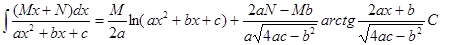 23. 23. 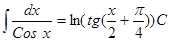 24. 24. 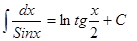 | |
| Екі айнымалы функция z = f(x, y). Экстремум | 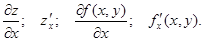 - бірінші ретті дербес туындылары - бірінші ретті дербес туындылары 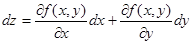 - толық дифференциал - толық дифференциал 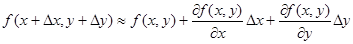 Дифференциал арқылы жуықтап есептеу Дифференциал арқылы жуықтап есептеу 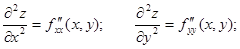 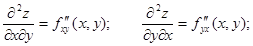 - екінші ретті дербес туындылары. Экстремумға зерттеу: 1) - екінші ретті дербес туындылары. Экстремумға зерттеу: 1) 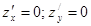 , P( , P( 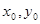 ) 2) егер ) 2) егер 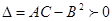 , мұндағы , мұндағы 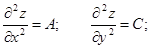 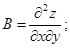 онда экстремум Р нүетсінде бар, егер онда экстремум Р нүетсінде бар, егер 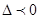 , онда экстермум болмайды. Егер , онда экстермум болмайды. Егер 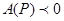 , онда P( , онда P( 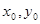 ) максимум . Егер ) максимум . Егер 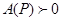 , онда P( , онда P( 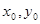 ) - минимум ) - минимум | |
| Екі еселі интеграл | 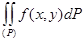 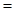 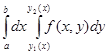 , , 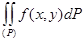 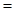 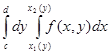 қайталаңған интегралға көшу қайталаңған интегралға көшу 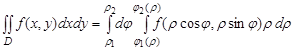 поляр координттарға көшу поляр координттарға көшу 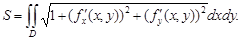 беттін ауданы беттін ауданы 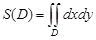 жазық фигураның ауданы жазық фигураның ауданы 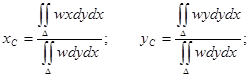 - ауыру центрі - ауыру центрі | |
| Үш еселі интеграл | 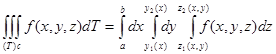 қайталаңған интегралға көшу қайталаңған интегралға көшу 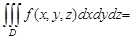 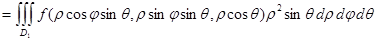 . Сфералық координаттарға көшу . Сфералық координаттарға көшу 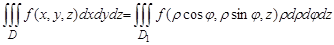 . Цилиндрлік координаттарға көшу . Цилиндрлік координаттарға көшу 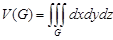 . – дененің көлімі . – дененің көлімі 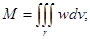 дененің массасы дененің массасы 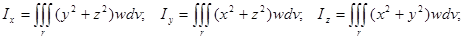 моменты инерции моменты инерции | |
| Қисық сызықты интегрладар | 1) Бірінші типті қисық сызықты интеграл. С қисығы еркінше параметрлік теңдеулермен берілсін  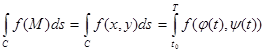 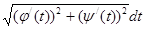 С қисығы айқындалған y=y(x) (a С қисығы айқындалған y=y(x) (a 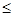 x x 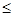 b) теңдеумен берілген b) теңдеумен берілген 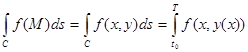 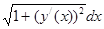 2) Екінші типті қисық сызықты интеграл. С =(AB) қисығы параметрлік 2) Екінші типті қисық сызықты интеграл. С =(AB) қисығы параметрлік  теңдеулермен берілген болсын. теңдеулермен берілген болсын.  Енді қисық айқындалған y=y(x) теңдеумен берілген Енді қисық айқындалған y=y(x) теңдеумен берілген 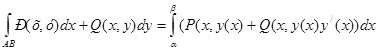 3) 3) 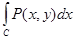 + + 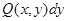 = = 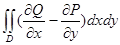 Грин формуласы. Грин формуласы. | |
| Беттік интегралдары | 1) Беттік интегралды екі еселі интегралға келтіру 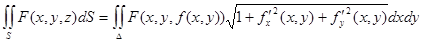 - Бірінші типті бетті к интегралы 2) - Бірінші типті бетті к интегралы 2) 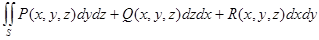 - Екiншi типті беттік интегралы 3) - Екiншi типті беттік интегралы 3) 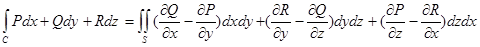 Стокс формуласы. 4) Стокс формуласы. 4) 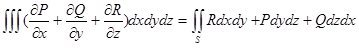 -Остроградский формуласы -Остроградский формуласы | |
| Фурье қатарлары | 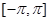 аралығында аралығында 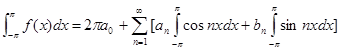 - Фурье қатары - Фурье қатары 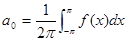 , , 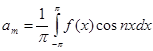 , , 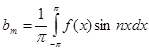 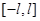 аралығында аралығында 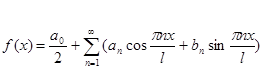 - Фурье қатары - Фурье қатары 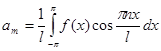 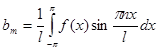 | |
| Өріс теориясының элементтері | 1) 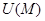 скаляр өріс берілсін. скаляр өріс берілсін. 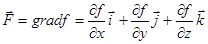 U скаляр шаманың градинент 2) U скаляр шаманың градинент 2) 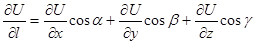 бағыты бойынша туындысы бағыты бойынша туындысы 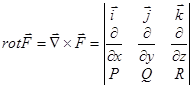 ротор деп аталады 3) ротор деп аталады 3) 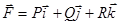 векторлық өрістің дивергенция векторлық өрістің дивергенция 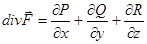 4) Онда Гаусс– Остроградский 4) Онда Гаусс– Остроградский 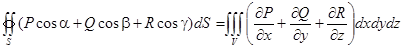
|
ДӘРІС ОҚУЛАР
Дәріс сабақтардың құрылымы
ДӘРІС. Цилиндрлік кесектің көлемі туралы есеп. Қос интегралдың анықтамасы. Қос интегралдың бар болуының шарты. Интегралданатын функциялар кластары. Қос интегралдардың қасиеттері.
1. Екі еселік интегралдың анықтамасы және есептеу. Жоғарғы жағынан z=f(x,y) бетпен, бүйір жағынан жасаушысы z осіне параллель цилиндрлік бетпен, ақырында, төменгі жағынан xy жазықтығындағы (P) жазық фигурамен қоршалған (V) дененні қарастырамыз. Осы дененің V көлемін табу керек.
Бұл есепті шешу үшін интегралдық есептеудегі дағдылы тәсілді қолданамыз: ізделетін шаманы элементар бөліктерге бөледі, әрбір бөлігін жуық есептейді, оларды жинақтап, соңынан шекке көшеді. Осы мақсатпен (P) (P1), (P2), …, (Pn) бөлшек облыстарға юөлеміз және осы бөлшек облыстары табаны болатын цилиндрлік бағандарды қарастырамыз. Бұл цилиндрлік жиыны берілген денені құрады.
Жеке бағандардың көлемін есептеу үшін әрбір (Pi) фигурадан еркінше бір 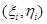 нүктеден аламыз. Егер әрбір бағанды жуықтап биіктігі f
нүктеден аламыз. Егер әрбір бағанды жуықтап биіктігі f 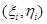 апликатаға тең нағыз цилиндр деп алсақ, онда бөлек бағанның жуық көлемі
апликатаға тең нағыз цилиндр деп алсақ, онда бөлек бағанның жуық көлемі
f 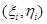 Pi
Pi
көбейтіндіге тең болады. Мұндағы Pi фигураның ауданы н көрсетеді. Бұл жағдайда барлық дененің көлемінің жуық өрнегі
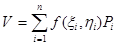 болады.
болады.
Бұл теңдіктің дәлдігін арттыру үшін (Pi) облыстардың санын көбейтіп, өлшемін кішірейтетін боламыз. (Pi) облыстардың ең үлкен диаметрі нольге ұмтылғандағы шегінде бұл дәл теңдік болып шығады, сондақтан
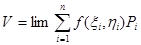 болады және есеп осымен шешіледі.
болады және есеп осымен шешіледі. 
f(x,y) осы түрдегі шек функциясынан (P) облысы бойында алынған қос интеграл болады. Ол мына символмен белгілінеді
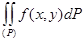

Жоғарғы көлем үшін табылған формула мына түрге келеді
V= 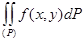
Қос интегралдың бар болуының шарты. Интегралданатын функция қажетті түрде шектелген болуы керек. Бұлай болмаған жағдайда кез келген тәсілмен (P) облысын бөлшек облыстарға бөлгенде , 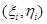 нүктелерді тандап алу есебінен интегралдық қосындыны қалауымызша үлкен етуге болады, сондықтан оның шектеулі I шегі болмай қалады.
нүктелерді тандап алу есебінен интегралдық қосындыны қалауымызша үлкен етуге болады, сондықтан оның шектеулі I шегі болмай қалады.
Берілген f(x,y) функциясының интегралдану шарттарын қарауға көшкенде, алдымен оны шектелген функция деп ұйғаратын боламыз 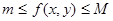 . Бір аінымалының функциясыжағдайындағыдай , бұл жерде де сондай ақ Дарбудың төменгі және жоғарғы қосындыларын енгізу қолайлы болады
. Бір аінымалының функциясыжағдайындағыдай , бұл жерде де сондай ақ Дарбудың төменгі және жоғарғы қосындыларын енгізу қолайлы болады 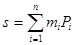 ,
, 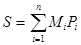 , мұндағы
, мұндағы 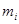 және
және 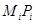 облысындағы f(x,y) функциясының мәндерінің дәл төменгі және дәл жоғарғы шекараларын белгілейді.
облысындағы f(x,y) функциясының мәндерінің дәл төменгі және дәл жоғарғы шекараларын белгілейді.
(P) облысы берілгени тәсілмен бөлшек облыстарға бөлінгенде 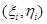 нүктелерінің таңдап алынуына байланыссыз, мына теңсіздіктер орындалатын болады
нүктелерінің таңдап алынуына байланыссыз, мына теңсіздіктер орындалатын болады 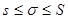 .
.
Дарбуның жоғарғы және төменгі қосындылары облысты бөлудің сол тәсіліне сәйкес интегралдық қосындылардың дәл жоғарғы және төменгі шекаралы болып табылады.
1 қасиет. Облысты бөлшек облыстарға бөлетін сызықтарға тағы жана сызықтар қосып , (Pi) бөлшектерді одан әрі ұсақтағанда, Дарбудың төменгі қосындысы кемімейді, ал жоғарғы қосындысы артпайды.
2 қасиет. Дарбудың әрбір төменгі қосындысы әрбір жоғарғы қосындысынан артпайды, тіпті бұл жоғарғы қосныдысы (P) облысын басқа тәсілмен бөлгеннен пайда болса да.
Теорема. Қос интеграл болу үшін 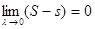 болуы қажетті және жеткілікті немесе басқаша белгілеулерде
болуы қажетті және жеткілікті немесе басқаша белгілеулерде
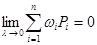 (1) ,
(1) ,
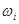 - мұнда f(x,y) функциясының (Pi) бөлшек облыстағы
- мұнда f(x,y) функциясының (Pi) бөлшек облыстағы 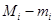 тербелесі.
тербелесі.
Интегралданатын функциялар кластары.
1. (P) облысындағы әрбір үздіксіз f(x,y) функциясы интегралданатын болады.
Расында, егер f(x,y) функциясы (P) облыста үздіксіз болса, онда бір қалыпты үздіксіздіктің қасиеті бойынша әрбір 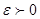 санына сәйкес
санына сәйкес 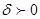 саны табылады және диаметрі
саны табылады және диаметрі 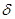 дан кіші (Pi) бөліктерге бөлінген болсын. Сонда барлық
дан кіші (Pi) бөліктерге бөлінген болсын. Сонда барлық 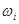 тербелістер
тербелістер 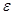 нен кіші болады және
нен кіші болады және 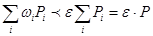 осыдан (1) шарттың орындалуы шығады.
осыдан (1) шарттың орындалуы шығады.
Лемма. (P) облыста ауданы 0 ге тең бір (L) қисығы берілсін. Сонда әрбір 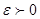 санына сәйкес
санына сәйкес 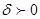 саны табылады және (P) облысы тек қана диаметрі
саны табылады және (P) облысы тек қана диаметрі 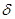 дан кіші бөліктерге бөлінгенде (L) қисығымен ортақ нұктелері болатындарының аудандарының қосындысы
дан кіші бөліктерге бөлінгенде (L) қисығымен ортақ нұктелері болатындарының аудандарының қосындысы 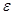 нен кіші болады.
нен кіші болады.
2. Егер шектелген f(x,y) функциясы тек ауданы 0 ге тең саны шектеулі қисықтарда үзілісті болса , онда ол интегралданатын болады.
Еркінше 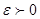 санын алайық. Ұйғару бойынша f(x,y) функциясының барлық «үзіліс сызықтарын» жалпы ауданы
санын алайық. Ұйғару бойынша f(x,y) функциясының барлық «үзіліс сызықтарын» жалпы ауданы 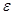 нен кіші болатын (Q) көп бұрышты облыстың ішіне орналастыруға болады. Саны шектеулі (L) сынық сызық облыстың шекарасы болады. Және оның да ауданы 0 ге тең болады.
нен кіші болатын (Q) көп бұрышты облыстың ішіне орналастыруға болады. Саны шектеулі (L) сынық сызық облыстың шекарасы болады. Және оның да ауданы 0 ге тең болады.
(P) ден ішкі (Q) облысын бөліп шығарғаннан кейін қалған тұйық облыста f(x,y) функциясы тұтасынан үздіксіз, демек , бір қалыпты үздіксіз. Сондықтан алдын ала берілген 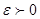 санына сәйкес
санына сәйкес 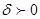 саны табылады және диаметрі
саны табылады және диаметрі 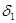 ден кіші осы облыстың әр бөлігінде f(x,y) функциясының тербілісі
ден кіші осы облыстың әр бөлігінде f(x,y) функциясының тербілісі 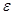 нен кіші болады.
нен кіші болады.
Енді лемма бойынша , оң 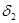 санын табуға болады, әр қашан (P) облысын еркінше қисықтармен диметрлері осы
санын табуға болады, әр қашан (P) облысын еркінше қисықтармен диметрлері осы 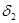 ден кіші болатын етіп бөліктерге бөлгенде , сол бөліктердің (L) сынығына тиісетіндерінің аудандарының қосындысы
ден кіші болатын етіп бөліктерге бөлгенде , сол бөліктердің (L) сынығына тиісетіндерінің аудандарының қосындысы 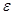 нен кіші болады.
нен кіші болады. 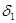 ,
, 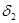 сандарының ең кіші
сандарының ең кіші 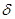 болсын. (P) облысын диметрлері
болсын. (P) облысын диметрлері 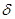 дан кіші болатын (P1), (P2), …, (Pn) бөліктерге бөлеміз және сәйкес
дан кіші болатын (P1), (P2), …, (Pn) бөліктерге бөлеміз және сәйкес 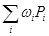 қосындыны қарастырамыз. Бұл қосынды екі қосындыға бөліп жазамыз
қосындыны қарастырамыз. Бұл қосынды екі қосындыға бөліп жазамыз
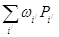 +
+ 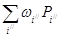
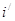 белгі тұтасымен (Q) облысының сыртында жататын
белгі тұтасымен (Q) облысының сыртында жататын 
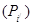 облыстарға сәйкес деп , ал
облыстарға сәйкес деп , ал 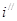 белгі қалған басқаларына сәйкес деп ұйғарамыз. Осы қосындыларын әрқайсысын жеке мұғдарлаймыз.
белгі қалған басқаларына сәйкес деп ұйғарамыз. Осы қосындыларын әрқайсысын жеке мұғдарлаймыз.
Сондықтан 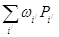
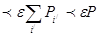 болады. Басқа жағынан егер барлық (P) облысындағы f(x,y) функциясының тербелісін
болады. Басқа жағынан егер барлық (P) облысындағы f(x,y) функциясының тербелісін 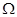 арқылы белгілесек , онда
арқылы белгілесек , онда 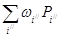
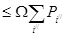 теңсізідігі табылады.
теңсізідігі табылады.
Ақырында 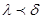 болғанда
болғанда 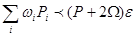 болып шығады. Бұл теңсіздіктің оң жағы
болып шығады. Бұл теңсіздіктің оң жағы 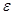 мен бірге еркінше аз болғандықтан (1) шарт орындалатын болады.
мен бірге еркінше аз болғандықтан (1) шарт орындалатын болады.
Қос интегралдың қасиеттері.
1. Егер ауданы 0 ше тең кейбір (L) сынығы бойында (P) облыста интегралданатын f(x,y) функциясының мәнін қалауымызша өзгертсек, онда жаңадан табылған фуекция да (P) облысында интегралданатын болады және оның интегралы f(x,y) функциясының интегралына тең болады.
2. Егер f(x,y) функциясы берілген (P) облысы ауданы 0 ге тең (L) қисығымен 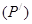 және
және 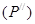 екі облысқа бөлінген болса, онда f(x,y) функциясының тұтас (P) облысында интегралданатындығынан оның
екі облысқа бөлінген болса, онда f(x,y) функциясының тұтас (P) облысында интегралданатындығынан оның 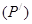 және
және 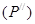 бөлшек облыстарында да интегралданатындығы келіп шығады және керсінше
бөлшек облыстарында да интегралданатындығы келіп шығады және керсінше 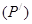 және
және 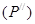 облыстарда функцияның интегралданатындығынан (P) облысында интегралданатындығы келіп шығады. Сонымен
облыстарда функцияның интегралданатындығынан (P) облысында интегралданатындығы келіп шығады. Сонымен 
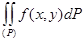
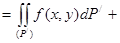
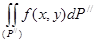 болады.
болады.
3. Егер (P) облысында интегралданатын f(x,y) функциясын тұрақты к ға тең көбейтсек, онда шығатын функция да сондай ақ интегралданатын болады және сонымен бірге 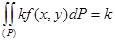
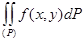 болады.
болады.
4. Егер (P) облысында f(x,y) және g(x,y) фунцкиялары интегралданатын болса, онда f(x,y) 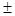 g(x,y) фунцкиясыда интегралданаьтын болады. Және
g(x,y) фунцкиясыда интегралданаьтын болады. Және 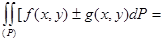
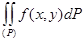
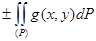 болады.
болады.
5. Егер (P) облысында интегралданатын f(x,y) және g(x,y) фунцкиялар үшін f(x,y) 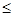 g(x,y) теңсізідігі орындалатын болса онда
g(x,y) теңсізідігі орындалатын болса онда 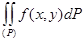
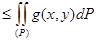 орындалады.
орындалады.
6. f(x,y) функциясы интегралданатын жағдайда 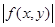 функциясы да интегралданатын болады және
функциясы да интегралданатын болады және 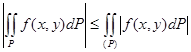 теңсізідігі орындалады.
теңсізідігі орындалады.
7. Егер (P) облысында интегралданатын f(x,y) функциясы 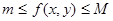 теңсізідікті қанағаттандыратын болса, онда
теңсізідікті қанағаттандыратын болса, онда 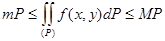 теңсіздігі орындалады.
теңсіздігі орындалады.
ДӘРІС. Қос интегралды есептеу. Тік бұрышты облыс жағдайында қос интегралды қайталанған интегралға келтіру. Қисық сызықты облыс жағдайында қос интегралды қайталанған интегралға келтіру
Бірінші семестрде дененің көлемін оның көлденеңқимасы бойынша есептеуге берілген есеппен кездестік. Осыған қатысты формуланы еске түсірейік. Дене 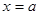 және
және 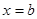 жазықтықтармен қоршалған болсын , х абциссаға
жазықтықтармен қоршалған болсын , х абциссаға 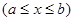 сәйкес болатын , х өсіне перпендикуляр жазықтықпен қиғандағы дененің қимасының ауданы
сәйкес болатын , х өсіне перпендикуляр жазықтықпен қиғандағы дененің қимасының ауданы 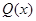 деп ұйғарайық. Сонда дененәң көлемі , бар болатын болса, мына формуламен өрнектеледі
деп ұйғарайық. Сонда дененәң көлемі , бар болатын болса, мына формуламен өрнектеледі 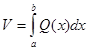 . Енді осы формуланы алдынғы сөз болған цилиндрлік кесектің көлемін есептеуге қолданамыз. Кесектің табаны
. Енді осы формуланы алдынғы сөз болған цилиндрлік кесектің көлемін есептеуге қолданамыз. Кесектің табаны 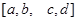 тік төртбұрыш болған жағдайдан бастаймыз.
тік төртбұрыш болған жағдайдан бастаймыз. 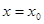
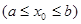 жазықтығы қиятын кесектің қимасы қисық сызықты трапеция болады. Оның ауданың табу үшін бұл фигураның проекциясын
жазықтығы қиятын кесектің қимасы қисық сызықты трапеция болады. Оның ауданың табу үшін бұл фигураның проекциясын 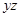 жазықтығына түсшреміз. Сонда өзімен тең трапециясын тауып аламыз. Қисық сызықты трапеция ауданының анықталған интеграл түріндегі белгілі өрнегімен пайдаланып, мынаны жазамыз
жазықтығына түсшреміз. Сонда өзімен тең трапециясын тауып аламыз. Қисық сызықты трапеция ауданының анықталған интеграл түріндегі белгілі өрнегімен пайдаланып, мынаны жазамыз 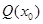
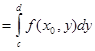 . Біздің болжауымыз кез келген қимаға жарамды болатындықтан , жалпы алғанда
. Біздің болжауымыз кез келген қимаға жарамды болатындықтан , жалпы алғанда 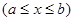 ушін
ушін 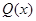
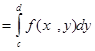 болады . Осы формуланы көлемін формулаға қойғанда мына формуланы табамыз V=
болады . Осы формуланы көлемін формулаға қойғанда мына формуланы табамыз V= 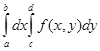 . Бірақ көлем V үшін біздін өрнегіміз де бар сондықтан
. Бірақ көлем V үшін біздін өрнегіміз де бар сондықтан 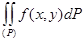 =
= 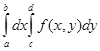 .
.
Сонымен қос интеграл қайталанған интегралға келтірілді. ХУ жазықтығындағы (Р) облысы 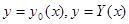
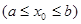 екі қисықпен және
екі қисықпен және 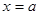 және
және 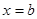 екі ординатамен қоршалған қисық сызықты трапеция болған жалпы жағдай үшін де осыған ұқсас нәтижені тауып алуға болады. Қарастырылыған жағдайданайырмасы тек мынау – бұрын кез келген белгілеп алынған
екі ординатамен қоршалған қисық сызықты трапеция болған жалпы жағдай үшін де осыған ұқсас нәтижені тауып алуға болады. Қарастырылыған жағдайданайырмасы тек мынау – бұрын кез келген белгілеп алынған 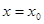 де у
де у 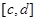 аралығында ғана өзгеретін еді, ал енді ол аралықтың өзі
аралығында ғана өзгеретін еді, ал енді ол аралықтың өзі 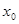 ге тәуелді болады
ге тәуелді болады 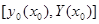 Сондықтан
Сондықтан 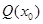
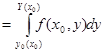 болады. Ақырында мынаны табамыз V=
болады. Ақырында мынаны табамыз V= 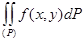 =
= 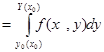 .
.
Тік бұрышты облыс жағдайында қос интегралды қайталанған интегралға келтіру.
Теорема. Егер (P) тік төртбұрышта (a 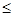 x
x 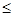 b, c
b, c 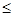 y
y 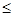 d) анықталған f(x,y) функциясы үшін
d) анықталған f(x,y) функциясы үшін
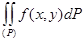 (1)
(1)
қос интегралы бар болса және a 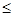 x
x 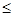 b интервалындағы х – тің әрбір тұрақты мәнінде жай интеграл
b интервалындағы х – тің әрбір тұрақты мәнінде жай интеграл
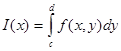 , (a
, (a 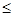 x
x 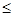 b) (2)
b) (2)
бар болса, онда сонымен қатар қайталанған интеграл 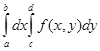 (3)
(3)
бар болады және 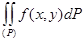
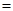
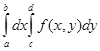 (4)
(4)
теңдік орындалатын болады.
Дәләлдеме. (P) тік төртбұрышта анықтайтын 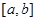 және
және 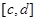 арақықтарды нүктелерімен бөліктерге бөлеміз
арақықтарды нүктелерімен бөліктерге бөлеміз
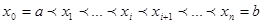
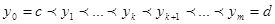 Сонда (P) тік төртбұрыш мынадай дербес
Сонда (P) тік төртбұрыш мынадай дербес 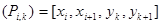 тік төртбұрыштарға бөлінеді.
тік төртбұрыштарға бөлінеді.
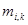 және
және 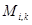 арқылы f(x,y) функциясының
арқылы f(x,y) функциясының 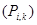 тік төртбұрыштағы сәйкес дәл төменгі және дәл жоғарғы шекараларын белгілейміз. Сондықтан осы тік төртбұрыштың барлық (x,y) нүктелері үшін
тік төртбұрыштағы сәйкес дәл төменгі және дәл жоғарғы шекараларын белгілейміз. Сондықтан осы тік төртбұрыштың барлық (x,y) нүктелері үшін 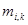
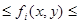
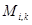 теңсізідігі орындалатын болады.
теңсізідігі орындалатын болады. 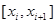 аралығынан х ті қалауымызша белгілеп алып :
аралығынан х ті қалауымызша белгілеп алып : 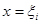 және у бойынша
және у бойынша 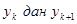 дейін интегралдап мына теңсіздігін табамыз
дейін интегралдап мына теңсіздігін табамыз 
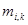
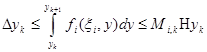
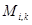 . Мұнда
. Мұнда 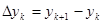 , у бойынша интеграл бар болады, себебі бүкіл
, у бойынша интеграл бар болады, себебі бүкіл 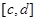 арақығында (2) интеграл бар деп ұйғарылған. Осыған ұқсас теңсіздіктерді к бойынша 0 ден
арақығында (2) интеграл бар деп ұйғарылған. Осыған ұқсас теңсіздіктерді к бойынша 0 ден 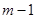 ге дейін жинақтап төменгі теңсіздікті табамыз
ге дейін жинақтап төменгі теңсіздікті табамыз 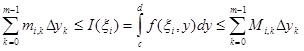
Егерде осы теңсіздіктердің барлық бөліктерін 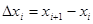 ге дейін жинақтайтын болсақ мынау шығады
ге дейін жинақтайтын болсақ мынау шығады 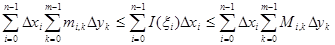
Ортада тұрған шама 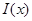 функциясы үшін интегралдық қосынды. Ал шеткі мүшелеріне келсек, олар (1) қос интеграл үшін Дарбудың s және S қосындылары болады.
функциясы үшін интегралдық қосынды. Ал шеткі мүшелеріне келсек, олар (1) қос интеграл үшін Дарбудың s және S қосындылары болады. 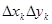 расында
расында 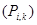 тік төртбұрыштың
тік төртбұрыштың 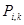 ауданы балғандықтан мысалы
ауданы балғандықтан мысалы 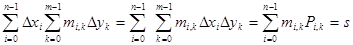 болады.
болады.
Сонымен ақтығында шығатыны 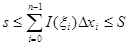 Егер енді
Егер енді 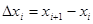 және
және 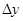 бір уақытта 0 ге ұмтылса , онда (1) қос интегралдың бар болуы себепті, s және S екі қосындының екеуі де қос интегралға шегі ретінде ұмтылатын болады. Мұндай жағдайда және
бір уақытта 0 ге ұмтылса , онда (1) қос интегралдың бар болуы себепті, s және S екі қосындының екеуі де қос интегралға шегі ретінде ұмтылатын болады. Мұндай жағдайда және 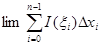 =
= 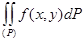 болады , яғни (1) қос интеграл сонымен бірге функциясының интеграл интегралы болып табылады.
болады , яғни (1) қос интеграл сонымен бірге функциясының интеграл интегралы болып табылады.
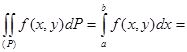
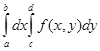 Сонымен теорема дәлелденді.
Сонымен теорема дәлелденді.

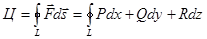 векторлық өрістін циркуляциясы
векторлық өрістін циркуляциясы