Распределение ТЕПЛОВОЙ энергии
По степеням свободы
Если степени свободы частицы входят в гамильтониан симметрично, то на каждую степень свободы приходится одинаковая тепловая энергия, обусловленная температурой.
Теорему предложил Дж. Уотерстон в 1845 г., количественное выражение дали Максвелл в 1860 г. и Больцман в 1868 г. Теорема применима для классических систем. Для квантовых систем теорема не выполняется.
Джеймс Клерк Максвелл (1831–1879)
Людвиг Больцман (1844–1906)
Гамильтониан частицы
Рассмотрим гамильтониан частицы идеального газа со степенными зависимостями от координат и импульсов
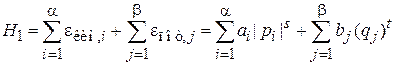, (2.38)
где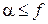 
– число активизированных степеней свободы с кинетической энергией, причем 
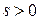; импульсы находятся в пределах 
; 
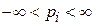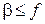– число активизированных степеней свободы с потенциальной энергией; координаты находятся в пределах 
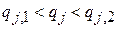. Для симметрии гамильтониана по j необходима независимость 
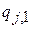и 
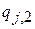от j.
Средние значения энергии частицы
При температуре Т
Преобразуем статистический интеграл частицы (2.19)
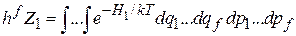
путем интегрирования по аргументу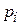 
по частям. Остальные интегралы оставляем без изменения. Полагаем
, 
,
, 
,
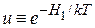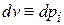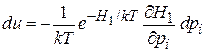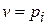тогда
.
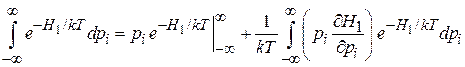Свободное слагаемое равно нулю за счет экспоненциальной функции. В результате
,
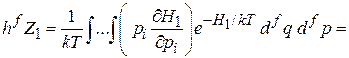
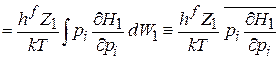где учтена функция распределения (2.16)
,
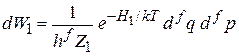и определение среднего
.
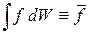В результате
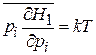. (2.38а)
При интегрировании по частям по аргументу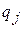 
в пределах от 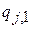до 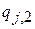, в общем случае, сохраняется свободное слагаемое
,
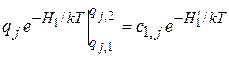где
.
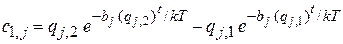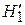отличается от 
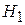отсутствием слагаемого потенциальной энергией с 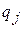. Выражение (2.19) для Z с гамильтонианом (2.38) является произведением независимых интегралов по каждому аргументы. В результате
,
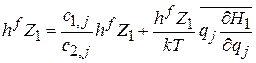где
,
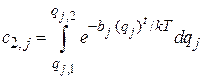тогда получаем
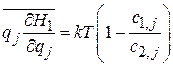. (2.38б)
В (2.38а) и (2.38б) подставляем гамильтониан
,
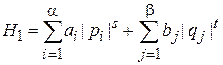где
, 
,
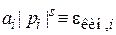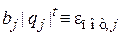получаем
,
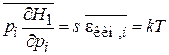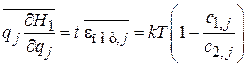. (2.38в)
При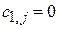 
с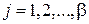 
, величины 
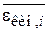и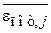 
не зависят от i и j, т. е. выполняется теорема о равном распределении тепловой энергии по степеням свободы. С учетом всех степеней свободы в этом случае находим
,
.
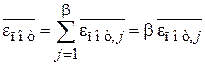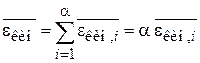Средние значения потенциальной, кинетической и полной энергий частицы пропорциональны температуре
,
,
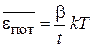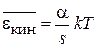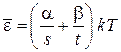. (2.39)
Примеры
1. Нерелятивистская свободная частица трехмерного газа при температуре T, движущаяся поступательно вдоль осей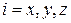 
, имеет
.
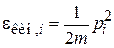Сравниваем с (2.38)
,
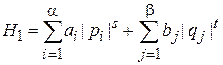в виде
,
находим
, 
.
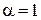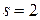Из (2.39) получаем
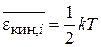. (2.40)
Для классического равновесного газа на каждую поступательную степень свободы частицы приходится тепловая кинетическая энергия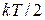 
.
2. Линейный гармонический осциллятор
.
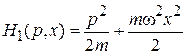Сравниваем с
,
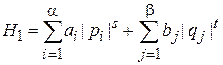получаем
, 
.
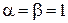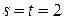С учетом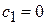 
из (2.39) находим
,
,
.
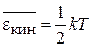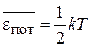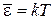На линейное гармоническое колебание осциллятора приходится тепловая энергия kT, которая складывается из кинетической и потенциальной энергий.
НЕУСТРАНИМАЯ ПОГРЕШНОСТЬ
ИЗМЕРИТЕЛЬНОГО ПРИБОРА
Макрохарактеристика равновесной системы остается постоянной только в среднем. Ее флуктуация вызвана хаотическими тепловыми движениями молекул.
Измерительное устройство испытывает тепловые колебания. Невозможно измерить физическую величину с точностью, меньшей амплитуды колебаний указателя прибора. Оценим неустранимую погрешность весов, работающих на основе упругой силы, используя теорему о распределении энергии по степеням свободы.