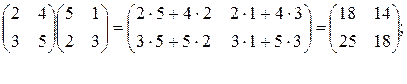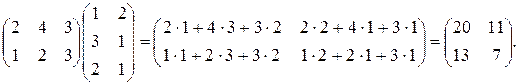Диагональная матрица имеет вид

2.

1. Системы двух и трех линейных уравнений с двумя и тремя неизвестными.

Линейным уравнением первой степени с 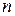неизвестными 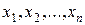называется уравнение вида

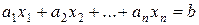(1)

Совокупность 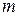линейных уравнений (1) называется системой 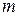линейных уравнений с 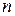неизвестными (или кратко линейной системой). Линейная система записывается следующим образом:

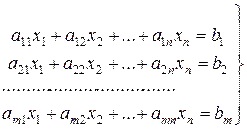(2)

Числа 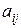, 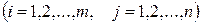называются коэффициентами линейной системы, числа 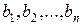- свободными членами системы.

Линейная система называется однородной, если все ее свободные члены равны нулю и неоднородной, если хотя бы один ее свободный член отличен от нуля.

Решением линейной системы (2) называется такая совокупность 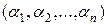из 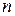чисел, которая при 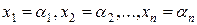каждое уравнение системы (2) обращает в тождество.

Система двух линейных уравнений с двумя неизвестными.

Запишем линейную систему двух уравнений с двумя неизвестными в следующем виде:

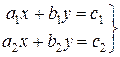(3)

Чтобы решить эту систему введем три определителя второго порядка

; ;

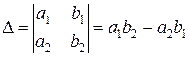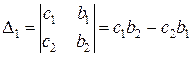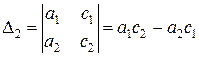
Определитель 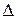называется определителем системы (3). Уравнения (4) и (5) дают систему уравнений, эквивалентную системе (3):

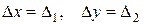(6)

Для решения системы (6) рассмотрим три случая:

1) 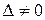. Следовательно:

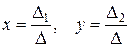(7)

Формулы (7) дают единственное решение линейной системы (3) и носят название формул Крамера для решения системы двух линейных уравнений с двумя неизвестными.

2) 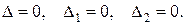В этом случае система (6), а, следовательно, и система (3) имеет бесчисленное множество решений.

Пример. Решить системы уравнений:

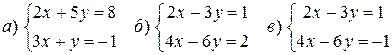
Решение. Вычислим определители :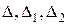

а)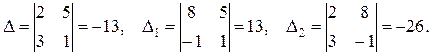

Так как 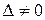, то формулы Крамера дают: .

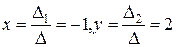Рассмотрим системы трех линейных уравнений с тремя неизвестными

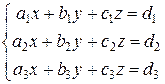(8)

Чтобы найти решение системы (8) введем четыре определителя третьего порядка:

;

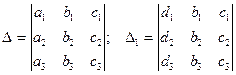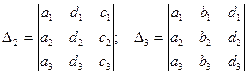
Определитель 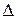называется определителем системы (8).

При 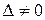получаем решение системы (8):

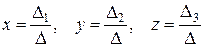(14)

Формулы (14) называются формулами Крамера для решения системы трех линейных уравнений с тремя неизвестными.

Примеры. Решить системы уравнений:

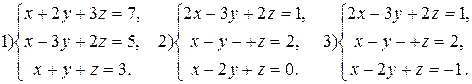
Решение.

1) Имеем:

;

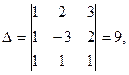
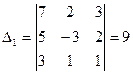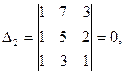
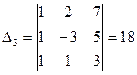
Формулы (14) дают: .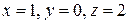

1. Действия над матрицами.

Множество чисел, расположенных в виде прямоугольной таблицы

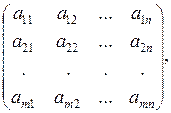(1)

имеющей m строк и n столбцов, называется прямоугольной матрицей размера m 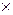n.

Числа, составляющие матрицу (1), могут быть как комплексными, так и вещественными и называются ее элементами.

Матрица называется в е щ е с т в е н н о й, если все ее элементы – вещественные числа.

Мы будем рассматривать, как правило, вещественные матрицы.

Если m=n , то матрица (1) называется к в а д р а т н о й матрицей порядка n.

Например, матрица

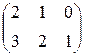
имеет размер 2 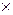3, а матрица

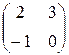
является квадратной матрицей порядка 2.

Квадратная матрица, у которой все элементы, расположенные вне г л а в н о й диагонали, идущей с левого верхнего угла в правый нижний, равны нулю, называется д и а г о н а л ь н о й матрицей.

Диагональная матрица имеет вид

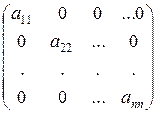
У диагональной матрицы все элементы с неравными индексами равны нулю, то есть 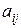=0, если i=j.

Диагональная матрица

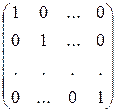
называется единичной матрицей и обозначается буквой Е

Для обозначения матриц будем использовать также прописные буквы латинского алфавита A, B, C, …, X,Y, … .

Матрица A= ( 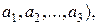состоящая из одной строки, называется

с т р о ч н о й матрицей длины n или в е к т о р – с т р о к о й; матрица

B= ,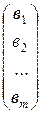

состоящая из одного столбца, называется с т о л б ц о в о й матрицей высоты m или в е к т о р – с т о л б ц о м.

Сложение матриц и умножение матрицы на число

Определение. Суммой двух матриц А и В одного и того же размера называется матрица С=А+В того же размера, элементы которой равны суммам соответствующих элементов данных матриц, то есть если

А= 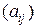, В=( 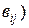и С=(с_ij), то с_ij=а_ij+в_ij,(i=1,2,…m, j=1,2,…n).

Пример. Пусть

А= 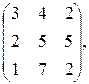В=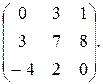

Тогда

С=А+В=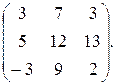

Определение. Произведением матрицы А=(а_ij) на число 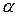(вещественное или комплексное) называется матрица 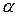А, элементы которой есть элементы матрицы А, умноженные на 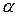, то есть

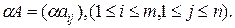
Произведение матриц

Определение. Произведением матрицы А=(а_ij) размера m 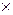n на матрицу В=(в_ij) размера n 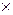p называется матрица С=АВ=(с_ij) размера m 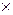p, где

с_ij=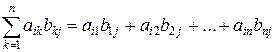

(i=1,2,…,m, j=1,2,…n).

Согласно этому определению, произведение двух матриц имеет смысл только тогда, когда число столбцов первой матрицы равно числу строк второй

матрицы. Отсюда, квадратные матрицы одного и того же порядка всегда можно перемножить.

В общем случае умножение двух матриц зависит от порядка сомножителей, то есть оно некоммутативно: АВ 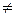ВА, (или даже ВА не имеет смысла).

Отметим легко проверяемое тождество:

АЕ=ЕА=А,

справедливое для любой квадратной матрицы А и единичной матрицы Е того же размера, что и матрица А.

Примеры.