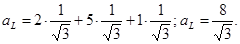Линейные операции над векторами в координатной форме

1. При умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

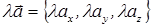
2. При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).

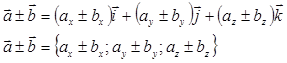
3. Векторы коллинеарны тогда и только тогда, когда их одноименные координаты пропорциональны.

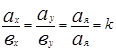
Зная проекции вектора 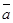, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно записать

,

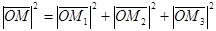т.е.

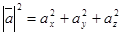(4)

Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат

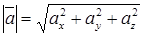(5)

Найдем координаты вектора 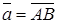, если известны координаты точек А(х₁;у₁;z₁) и В(х₂;у₂;z₂) (рис.5).

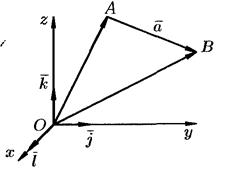
Рис. 5

= .

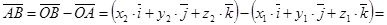
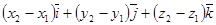Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала

.

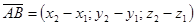Пример 1.

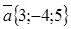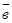
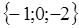По данным векторам и найти координаты вектора .

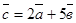Решение:

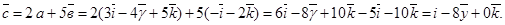
Вектор 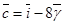. Координаты вектора .

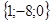Пример 2.

Проверить коллинеарность векторов 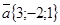и .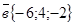

Решение:

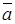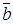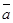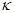
Если векторы и коллинеарны, то должно выполняться условие = 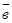или в координатной форме

.

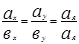Для заданных векторов .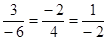

Следовательно, векторы 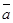и 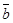коллинеарны.

При этом 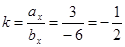и 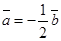, то есть модуль вектора 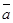равен 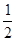модуля 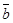. Знак «–» указывает, что векторы направлены в противоположные стороны.

Направляющие косинусы

Пусть углы вектора 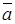с осями ОX, ОY и ОZ соответственно равны α, β, γ. По свойству проекции вектора на ось, имеем

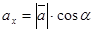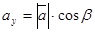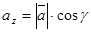(6)

Или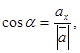

.

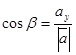
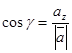Числа 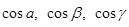называются направляющими косинусами вектора .

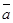Подставив выражение (6) в равенство (4), получим

.

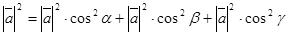Сократив на 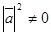, получим соотношение

,

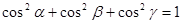т.е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

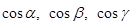Координатами единичного вектора являются числа , т.е. .

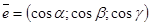Задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.

Пример 3.

Проекции вектора 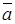на оси координат равны a_x=1, a_y=–4, a_z=8. Найти длину вектора 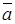, его направляющие косинусы.

Решение:

По формуле 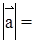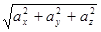имеем .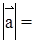

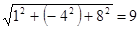Используя формулы

, ,

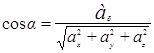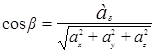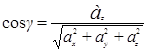
находим направляющие косинусы вектора

.

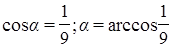
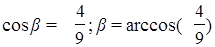
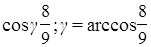Пример 4.

Найти равнодействующую двух сил 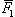и 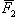, модули которых равны F₁ = 5, F₂ = 7, угол между ними θ = 60^°.

Решение:

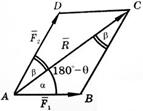
По формуле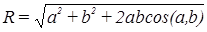

находим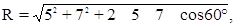

Пример 5.

Даны два вектора: 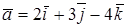и 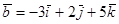. Найти проекции на координатные оси суммы и разности этих векторов.

Решение:

Составим сумму и разность этих векторов:

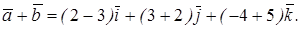
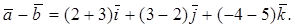
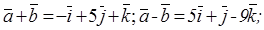
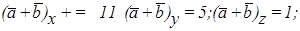
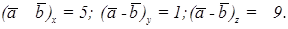
Пример 6.

Дан вектор. 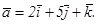Найти его проекцию a_L на ось L, составляющую с координатными осями равные острые углы.

Решение:

По условию направляющие косинусы оси проекций между собой равны:

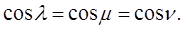
Но сумма квадратов направляющих косинусов какого-либо направления равна 1, а потому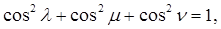

Так как в этой сумме все слагаемые между собой равны, то

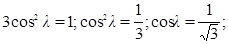
Тогда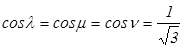

Знак «+» перед корнем взят потому, что по условию углы λ, μ и ν – острые, а значит, косинусы их положительны.

Так как по условию a_x = 2; a_y = 5; a_z = 1, то по формуле

a_L=a_xcos λ+cos μ+cosν

Получаем