Равносильные формулы. Свойства
Два высказывания называются равносильными, если равны их истинностные функции, рассматриваемые как функции от всех значений переменных, т.е. на каждом наборе значений оба высказывания принимают одинаковые значения.
Основные равносильности:
1. Коммутативность.
а) 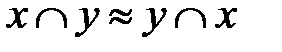 (для конъюнкции);
(для конъюнкции);
б) 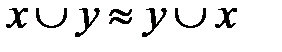 (для дизъюнкции).
(для дизъюнкции).
2. Ассоциативность.
а) 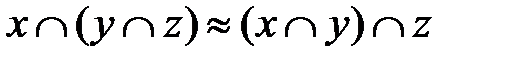 (для конъюнкции);
(для конъюнкции);
б) 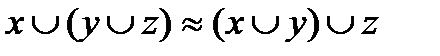 (для дизъюнкции).
(для дизъюнкции).
3. Дистрибутивность.
а) 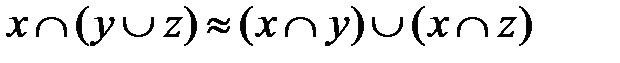 (для конъюнкции относительно дизъюнкции);
(для конъюнкции относительно дизъюнкции);
б) 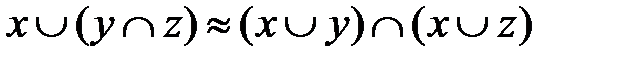 (для дизъюнкции относительно конъюнкции).
(для дизъюнкции относительно конъюнкции).
4. Закон де Моргана.
а) ┐ 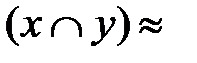 ┐
┐ 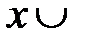 ┐
┐ 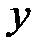 (отрицание конъюнкции есть дизъюнкция отрицаний);
(отрицание конъюнкции есть дизъюнкция отрицаний);
б) ┐ 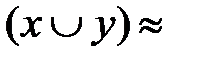 ┐
┐ 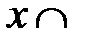 ┐
┐ 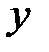 (отрицание дизъюнкции есть конъюнкция отрицаний).
(отрицание дизъюнкции есть конъюнкция отрицаний).
5. Идемпотентность.
а)  (для конъюнкции);
(для конъюнкции);
б)  (для дизъюнкции).
(для дизъюнкции).
6. Поглощение.
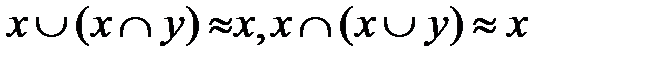 .
.
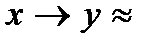 ┐
┐ 
7. Расщепление (склеивание).
а) 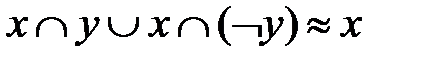 (1–ый закон расщепления);
(1–ый закон расщепления);
б) 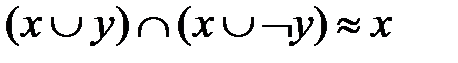 (2–ой закон расщепления).
(2–ой закон расщепления).
8. Двойное отрицание.
┐┐х=х
9. Свойства констант.
а) 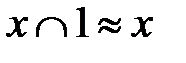
б) 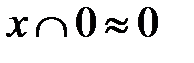
в) 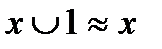
г) 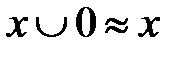
д) 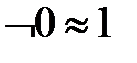
е) 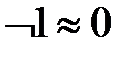 .
.
10. Закон противоречия.
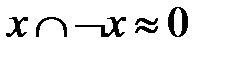
11. Закон “исключенного третьего”.
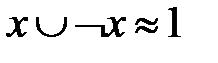
Каждая из перечисленных равносильностей может быть доказана с помощью таблиц значений функций, составленных для выражений, стоящих слева и справа от символа “ 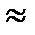 ”. Докажем, например, равносильность 4а. Для этого составим таблицу.
”. Докажем, например, равносильность 4а. Для этого составим таблицу.
Таблица
| х | у | 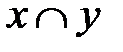 | 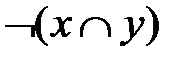 | 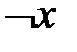 | 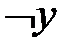 | 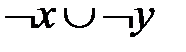 Ø Ø |
Из таблицы видно, что 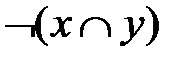 º
º 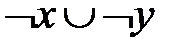 Ø, что и требовалось доказать.
Ø, что и требовалось доказать.
Прямая, обратная и противоположная теоремы
Рассмотрим четыре теоремы:
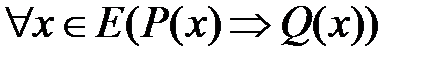 , (1) , (1) 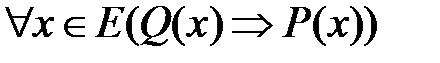 , (2) , (2) | 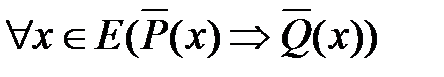 , (3) , (3) 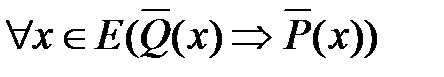 . (4) . (4) |
Определение 1: Пара теорем, у которых условие одной является заключением второй, а условие второй является заключением первой, называются взаимно обратными друг другу.
Так, теоремы (1)и (2), а также (3) и (4)- взаимно обратные теоремы. При этом, если одну из них называют прямой теоремой, то вторая называется обратной.
Определение 2: Пара теорем, у которых условие и заключение одной являются отрицанием соответственно условия и заключения другой, называются взаимно противоположными.
Так, теоремы (1) и (3), а также (2) и (4) являются взаимно противоположными теоремами.
Например, для теоремы
“Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником ” (1) обратной является теорема
“Если четырехугольник является прямоугольником, то его диагонали равны” (2).
Для теоремы (1) противоположной является теорема
“Если в четырехугольнике диагонали не равны, то четырехугольник не является прямоугольником” (3),
а для теоремы (2) противоположной является теорема
“Если четырехугольник не является прямоугольником, то его диагонали не равны ” (4).
В рассмотренном примере теоремы (1) и (4) являются одновременно ложными, а теоремы (2) и (3) одновременно истинными. Контрпримером к теореме (1) является равнобочная трапеция.
Ясно, что прямая и обратная теоремы, вообще говоря, не равносильны, т. е. одна из них может быть истинной, а другая – ложной. Однако легко показать, что теоремы (1) и (4), а также (2) и (3) всегда равносильны.
Действительно:
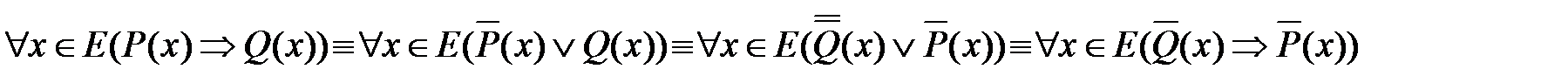 Из этих равносильностей следует, что, если доказана теорема (1), то доказана и теорема (4), а если доказана теорема (2), то доказана и теорема (3).
Из этих равносильностей следует, что, если доказана теорема (1), то доказана и теорема (4), а если доказана теорема (2), то доказана и теорема (3).
