Собственные числа и собственные векторы

Определение 19.3 Ненулевой вектор называется собственным вектором линейного преобразования , соответствующим собственному числу , если .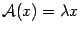

Совокупность всех собственных чисел линейного преобразования конечномерного линейного пространства называется спектром преобразования .

Вместо слов "собственное число" говорят также собственное значение, характеристическое число или характеристическое значение.

Если 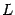-- двумерное или трехмерное линейное пространство, то собственный вектор линейного преобразования -- это такой вектор, что его образ коллинеарен самому вектору. Иными словами, после применения преобразования (в вещественном случае) может измениться длина вектора, а направление или сохранится, или изменится на противоположное, или вектор станет равным нулю (в случае ).

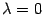В примере 19.1 любой вектор является собственным вектором линейного преобразования соответствующим собственному числу 2. В примере 19.2 при не кратном 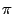преобразование не имеет собственных векторов, так как после применения преобразования длина каждого вектора не меняется и ни один вектор не сохраняет своего направления и не меняет направление на противоположное.

Пример 19.7 Пусть 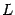-- двумерное векторное пространство, -- некоторая прямая, проходящая через начало координат, -- преобразование, переводящее каждый вектор в вектор , симметричный исходному относительно прямой (рис. 19.5). Тогда из векторов рисунка 19.5 собственным вектором преобразования будет вектор 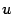, он соответствует собственному числу 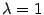, и вектор 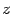, который соответствует собственному числу 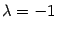. Читатель без труда поймет, что любой ненулевой вектор, лежащий на прямой , будет собственным вектором, соответствующим собственному числу 1, а любой ненулевой вектор, лежащий на прямой перпендикулярной и проходящей через начало координат, является собственным вектором, соответствующим собственному числу .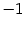

Предложение 19.2 Пусть -- собственный вектор линейного преобразования , соответствующий собственному числу и пусть -- ненулевое число. Тогда 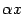-- тоже собственный вектор линейного преобразования , соответствующий собственному числу .

Доказательство.

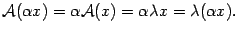
Пример 19.8 Пусть 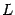-- двумерное векторное пространство, -- некоторая прямая, проходящая через начало координат, -- преобразование, переводящее каждый вектор в его проекцию на прямую (рис. 19.6). Очевидно, что любой ненулевой вектор, лежащий на прямой , будет собственным вектором, соответствующим собственному числу 1, а любой ненулевой вектор на прямой перпендикулярной и проходящей через начало координат, будет собственным вектором, соответствующим собственному числу 0.

Пример 19.9 Пусть -- линейное преобразование примера 19.3. Очевидно, что векторы, являющиеся многочленами нулевой степени, то есть числами, будут собственными векторами, соотвествующими собственному числу 0.

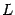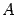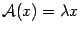Если в пространстве задан базис, то линейному преобразованию соответствует матрица . Пусть -- собственный вектор преобразования , соответствующий собственному числу , -- координатный столбец вектора . Тогда равенство означает, что .

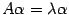Определение 19.4 Ненулевая матрица-столбец называется собственным вектором квадратной матрицы 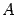, соответствующим собственному числу , если выполнено равенство .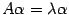

Замечание 19.2 Между собственными числами (собственными векторами) матрицы и линейного преобразования есть некоторое различие. Линейное преобразование вещественного линейного пространства может не иметь собственных векторов и, соответственно, собственных чисел. Матрица же, как увидим дальше, всегда имеет хотя бы одно собственное число, быть может комплексное, и ему соответствует собственный вектор (тоже, быть может, комплексный). Но если рассматривать линейные преобразования 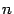-мерных комплексных пространств, то собственные числа преобразований совпадают с собственными числами матриц и собственные векторы преобразований имеют координатными столбцами собственные векторы матриц.

Предложение 19.3 Если две матрицы подобны, то наборы собственных чисел у них одинаковы.

Доказательство. Пусть 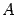и 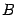-- две подобные матрицы порядка 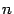. Рассмотрим 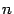-мерное комплексное линейное пространство. Выберем в нем базис 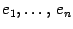и рассмотрим линейное преобразование , которое в этом базисе имеет матрицу 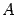. По следствию 19.1 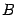будет матрицей того же преобразования в другом базисе. 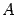Так как собственные числа линейного преобразования не зависят от выбора базиса, то спектр (набор собственных чисел) преобразования будет совпадать со спектрами матриц и .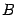

Вперед: Нахождение собственных чисел и собственных векторов матриц Наверх: Линейные преобразования Назад: Изменение матрицы линейного преобразования при изменении базиса