Метод замены плоскостей проекций
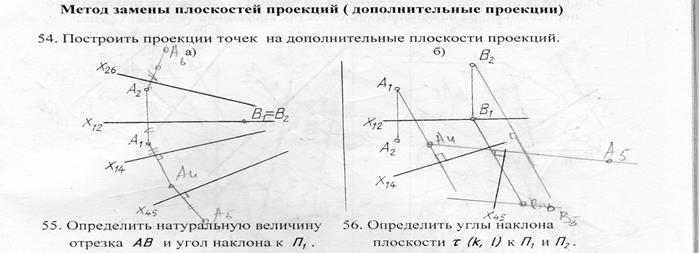
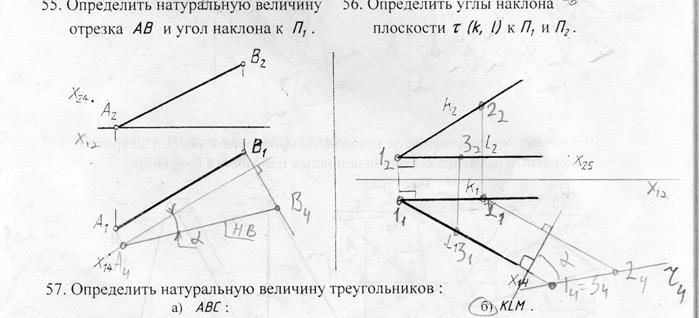
Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П1 или П2 новой плоскостями П4 (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.
Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.

11. Метод замены плоскостей проекций
Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П1 или П2 новой плоскостями П4 (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.
Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
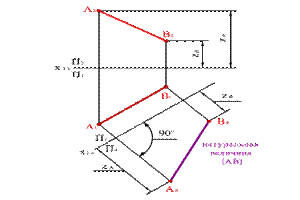
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.

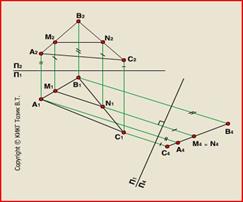
Алгоритм графических построений:
Проводим проекцию M2N2 некоторой прямой, принадлежащей плоскости АВС: M2N2 || П1П2;
Проводим линии проекционной связи и находим проекцию M1N1 этой прямой на П1;
Проводим ось проекций П1П4 на произвольном расстоянии и перпендикулярно M1N1;
Проводим линии проекционной связи в системе плоскостей проекции П1П4 перпендикулярно оси П1П4;
Откладываем на них от оси П1П4 расстояния равные расстояниям от А2, B2, C2 и M2N2 до оси П1П2;
Соединяем точки и получаем проекцию плоскости ABC на П4.
Угол a наклона С4А4В4 к оси П1П4 равен углу наклона плоскости АВС к П1. К решению подобной задачи сводится решение задач на определение углов наклона плоскости к плоскостям проекций П1 и П2, расхождение расстояний от точки до плоскости, между параллельными плоскостями, плоскостью и параллельной ей прямой и многие другие метрические и позиционные задачи.

