Уравнение подобия конвективного переноса тепла

КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

- процесс распространения тепла в жидкости (газе) от поверхности твердого тела или к поверхности его одновременно конвекцией теплопроводностью. Такой случай распространения тепла называю теплоотдачей. При теплоотдаче тепло распространяется от поверхности твердого тела к жидкости через пограничный слой за счет теплопроводности и от пограничного слоя в массу (ядро) жидкости преимущественно конвекцией. Очевидно, что на теплоотдачу существенное влияние оказывает характер движения жидкости.

Свободное движение жидкости (естественная конвенция) возникает вследствие разности плотностей нагретых и холодных частиц жидкости и определяется физическими свойствами жидкости, ее объемом и разностями температур нагретых и холодных частиц. Вынужденное (принудительное) движение жидкости возникает под действием какого-либо возбудителя (насоса, вентилятора) и определяется физическими свойствами жидкости, ее скоростью, формой и размерами канала, в котором осуществляется движение. При турбулентном движении жидкости теплообмен происходит интенсивнее, чем при ламинарном.

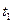Закон Ньютона. Основным законом теплоотдачи является закон Ньютона, согласно которому количество тепла dQ, переданное от теплообменной поверхности к окружающей среде (или от окружающей среды к теплообменной поверхности) прямо пропорционально поверхности теплообмена dF, разности температур поверхности и окружающей среды и времени , в течение которого осуществлялся теплообмен:

, (1)

где 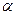коэффициент пропорциональности, который называют коэффициентом теплоотдачи.

Коэффициент теплоотдачи показывает, какое количество тепла передается от теплообменной поверхности к 1 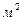в окружающую среду или, наоборот, от окружающей среды к теплообменной поверхности 1 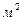в единицу времени при разности температур теплообменной поверхности и окружающей среды 1 град.

Определение коэффициента теплоотдачи сопряжено с трудностями, так как на теплоотдачу влияет много факторов: режим и скорость движения жидкости, физические параметры жидкости, форма и размеры теплообменной поверхности и др. Поэтому для проведения расчетов необходимо располагать уравнением, которое связывало бы значение коэффициента теплоотдачи с переменными, выражающими условия конвективного теплообмена. Таким уравнением является дифференциальное уравнение конвективного переноса тепла, дополненное уравнением, характеризующим условия на границе раздела жидкости и твердого тела.

Дифференциальное уравнение конвективного переноса тепла. При конвективном теплообмене тепло распространяется в жидкости одновременно теплопроводностью и конвекцией. Процесс математически описывается дифференциальным уравнением теплопроводности

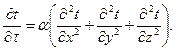(2)

Левая часть этого уравнения представляет локальное изменение температуры элемента в среде.

При конвективном теплообмене элемент перемещается из одной точки пространства в другую. Если обозначить скорости перемещения элемента в пространстве в направлении осей 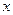, у и z соответственно через 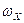, 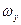и , то субстанциальная производная, характеризующая полное изменение температуры этого элемента, может быть записана:

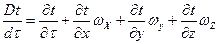. (3)

где 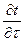- локальное изменение температуры,

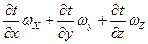конвективное изменение температуры.

Если в уравнении теплопроводности заменить локальное изменение температуры полным, то в результате получим дифференциальное уравнение конвективного переноса тепла Фурье - Кирхгофа:

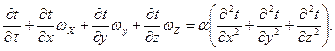(4)

Это уравнение является математическим описанием процесса распространения тепла в движущейся среде одновременно теплопроводностью и конвекцией, но для полного математического описания процесса конвективного теплообмена оно должно быть дополнено уравнением, характеризующим условия на границе раздела движущейся среды и твердого тела.

У поверхности твердого тела, находящегося в движущейся среде, всегда имеется пограничный слой толщиной б (рис. 1) через который тепло распространяется теплопроводностью. Количество этого тепла можно определить по закону Фурье:

.

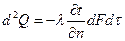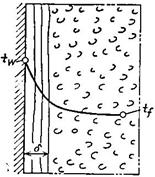
Рис.1. Характер изменения температуры в движущейся среде при конвективном теплообмене

Это же количество тепла можно найти по закону Ньютона:

Приравнивая одну к другой правые части последних равенств, Получаем уравнение, характеризующее условия на границе:

(5)

Уравнения (4) и (5) полностью описывают процесс конвективного теплообмена, но для большинства встречающихся на практике случаев они не разрешимы, поэтому не могут быть применимы для определения численных значений коэффициентов теплоотдачи.

Уравнение подобия конвективного переноса тепла

В расчетной практике пользуются уравнением подобия, полученным из этих уравнений методами теории подобия.

Из уравнения (5) делением обеих его частей на левую часть получают безразмерный комплекс, из которого выражают

число Нуссельта

Из дифференциального уравнения конвективного переноса тепла делением всех членов уравнения на получаем безразмерные комплексы, после сокращений которых получают

число Фурье и число Пекле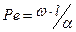

Полученные числа Nu, Fо и Ре являются числами теплового подобия. Число Нуссельта характеризует интенсивность теплообмена на границе раздела фаз. Число Фурье характеризует связь между скоростью изменения температурного поля, размерами и физическими характеристиками среды в нестационарных тепловых процессах. Число Пекле характеризует отношение количеств тепла, распространяемых в потоке жидкости конвекцией и теплопроводностью. Число Пекле обычно представляют в виде произведения двух чисел подобия:

Число Rе является числом гидродинамического подобия, а число Прандтля Рг характеризует поле теплофизических величин потока жидкости; его находят только по теплофизическим параметрам жидкости:

В случаях, когда теплообмен происходит в результате естественной конвекции, обусловленной разностью плотностей жидкости в различных точках системы, процесс характеризуется значением числа Архимеда

,

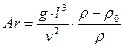где ρ и 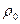плотности холодной и нагретой жидкости.

Поскольку в тепловых процессах разность плотностей в различных точках системы обусловливается разностью температур нагретой и холодной жидкости, комплекс в числе Архимеда заменяют произведением 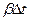(где 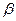-температурный коэффициент объемного расширения жидкости) и получают число Грасгофа ,

Число Грасгофа характеризует гидродинамический режим потока жидкости в условиях естественной конвекции, происходящей под влиянием разности плотностей нагретой и холодной жидкости

Полученный числа подобия дают возможность найти уравнения подобия конвективного переноса тепла:

Из чисел подобия этого уравнения только число Нуссельта не составлено целиком из условий однозначности, поэтому оно является определяемым числом подобия. На этом основании уравнение записывается в следующем виде: .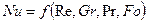

При стационарном процессе теплообмена из уравнения подобия выпадаетчисло Fo, и оно имеет вид:

При вынужденном движении потока, когда естественной конвекцией жидкости можно пренебречь, из уравнения подобия исключают число Грасгофа: 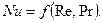или

При свободном движении жидкости (в условиях естественной конвекции) из уравнения подобия исключают число Рейнольдса:

или .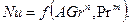

При решении конкретных задач по найденному из соответствующего уравнения подобия значению числа Нуссельта легко определяется коэффициент теплоотдачи:

.

С помощью полученных уравнений подобия обработано большинство опытных данных по конвективному теплообмену. На основании этих данных можно определить значение коэффициентов теплоотдачи для всех основных случаев теплообмена.