Построение интервальных рядов распределения случайной величины

Для группировки совокупности непрерывных случайных величин выборка исходных данных ранжируется в порядке убывания или возрастания величин и разбивается на интервалы (или градации, группы).

Последовательность операций при построении интервального ряда распределения:

1). Определение объема выборки n (длины ряда), т.е. числа значений случайных величин в исследуемой выборке.

2). Ранжирование данных – расположение всех значений случайных величин ряда в порядке возрастания (или убывания).

3). Определение крайних значений выборки (ряда) – минимального X_min и максимального X_max значения случайной величины Х_i.

4). Определение амплитуды (размаха) вариации, т.е. величины диапазона изменения значений СВ в исследуемой совокупности

А = Х_мах – Х_min

5). Определение количества интервалов (градаций).

Критерий определения числа градаций k в выборке учитывает объем выборки n:

или

Число данных (n)
Оптимальное число градаций (k)

Если число градаций будет отличаться от указанного возможного, то вычисления частоты для отдельных градаций будет ненадежным. Выбор слишком малого числа градаций затушевывает важные детали в распределении частот, использование слишком большого числа градаций не дает возможности достаточно хорошо упорядочить и обобщить данные.

Когда определено число градаций, то следует определить интервалы группировки.

6). Определение ширины интервалов.

Интервал – это значение группировочного признака, лежащее в определенных границах. Каждый интервал имеет свою ширину (размер), нижнюю и верхнюю границы или хотя бы одну из них. Нижней границей называется наименьшее значение признака в интервале, а верхней границей – наибольшее значение признака в интервале. Верхняя и нижняя границы градаций называются граничными значениями.

Интервалы группировок могут быть в зависимости от их величины равными и неравными. Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами. При выборе равных по величине градаций (мы будем заниматься именно этим типом градаций) нужно руководствоваться следующими соображениями:

Ширина (или размер) градации h представляет собой разность между верхней и нижней границами интервала. В случае равных интервалов ширина градации h определяется по следующей формуле

,

Интервалы группировок могут быть закрытыми и открытыми. Закрытыми называются интервалы, у которых имеются нижняя и верхняя граница. У открытых интервалов указана только одна граница: верхняя – у первого и нижняя – у последнего.

7). Выбор правила формирования градаций ( [… ) или (…] ): градации не должны перекрываться, т.е. каждое значение случайной величины может войти только в одну градацию.

Формирование градаций в соответствии с принятым правилом.

8). Определение центральных значений градаций. В интервальном ряду градации значений СВ заменяются центром (серединой) X_i соответствующих градаций.

9). Распределение значений СВ по градациям. После того, как градации выбраны, все данные исходной выборки распределяются по соответствующим градациям.

Подсчет количества значений СВ, попавших в каждую градацию с учетом правила формирования градаций, т.е. частот.

Частота (абсолютная повторяемость) m_i– это число значений СВ, вошедших в данную градацию из общей совокупности n.

Объем выборки после разнесения СВ по градациям не должен измениться!!

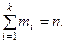
10). Расчет вероятностей появления значений СВ в каждом интервале.

Вероятность (относительная повторяемость) Р_i – это относительная частота соответствующего интервала (градации)

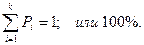
Для статистического ряда распределения могут рассчитываться дополнительно следующие показатели: