Микроканоническое распределение

Основные понятия и определения

Объект – изолированный равновесный идеальный газ из N частиц в объеме V с полной энергией E, т. е.

.

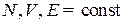Изолированный газ – через границу объема не переходят частицы и энергия.

Равновесный газ – макрохарактеристики не зависят от времени.

Идеальный газ – частицы независимы друг от друга, имеют малые размеры, не взаимодействуют на расстоянии.

Распределение микросостояний по фазовому пространству

Система изолирована, тогда

.

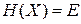Следовательно:

фазовый ансамбль находится в фазовом пространстве на гиперповерхности ;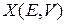

функция микроканонического распределения является дельта-функцией

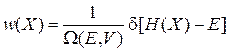. (2.7)

Условие нормировки (2.4)

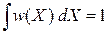
дает нормировочную постоянную

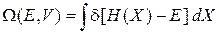. (2.8)

Выразим 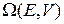через характеристики энергетического спектра состояний.

Энергетическая плотность состояний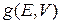

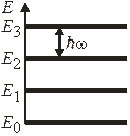
Набор возможных значений энергии системы называется спектром. Физическая система, находящаяся в ограниченном объеме, имеет дискретный спектр энергии. Пример показан на рисунке.

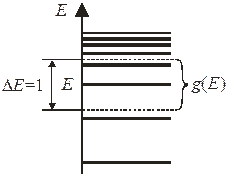
Спектр энергии зависит от объема сосуда, занятого системой, от соотношения между энергией и импульсом частицы.

Энергетическая плотность состояний 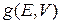есть число состояний в единичном интервале энергииоколо значения E. Это число уровней энергии, попадающих в интервал .

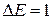Число состояний равно безразмерному объему фазового пространства 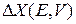внутри замкнутой гиперповерхности 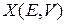, точки которой удовлетворяют уравнению 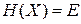. Увеличение энергии системы на 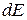сдвигает гиперповерхность в фазовом пространстве, увеличивает объем внутри нее и число состояний на величину

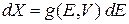. (2.9)

Тогда 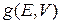есть изменение фазового объема 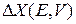, охватываемого гиперповерхностью 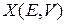, при изменении энергии на единицу

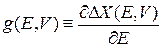, (2.9а)

где

.

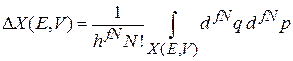Пример

Для гармонического осциллятора выполняется (П.2.4)

,

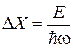тогда из (2.9а) получаем

.

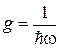Энергетическая плотность состояний осциллятора обратно пропорциональна частоте, не зависит от объема и энергии. Результат согласуется со спектром осциллятора (П.2.4а)

,

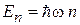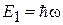– интервал эквидистантного спектра осциллятора.

Нормировочная постоянная

В выражение (2.8)

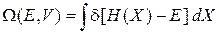
подставляем (2.9)

,

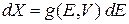­получаем

.

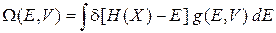Фильтрующее свойство дельта-функции снимает интеграл и дает

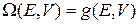. (2.10)

Нормировочная постоянная микроканонического распределения равна энергетической плотности состояний.

Микроканоническое распределение

Из (2.7)

,

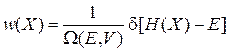и (2.10) получаем функцию распределения микросостояний по фазовому пространству

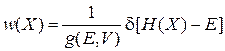. (2.10а)

Выразим термодинамические характеристики макросостояния через особенности распределения микросостояний по фазовому пространству.