Определение и свойства ОИ.

Задачи, приводящие к понятию определенного интеграла

Задача 1. Найти массу тонкого прямолинейного стержня длины l с переменной линейной плотностью.

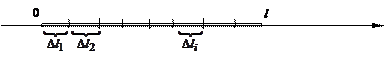Решение. Стержень тонкий – это значит, что поперечные размеры его столь малы по сравнению с длиной, что ими можно пренебречь. Предположим, что зависимость плотности от расстояния точки стержня до одного из его концов известна и может быть описана некоторой функцией. Составим математическую модель задачи следующим образом. Будем интерпретировать стержень с отрезком оси ОХ длины l , например с отрезком [0, l]. Тогда переменная плотность масс точек стержня есть функция переменной хÎ[0, l], обозначим ее r(х). Разобьем отрезок [0, l] на п произвольных частей и обозначим длины этих частичных отрезков Dl_i, i = 1,...,n.

Будем полагать, что п достаточно велико , а Dl_i достаточно малы. На каждом из этих отрезков разбиения возьмем произвольную точку x_i и в силу малости длины Dl_i можем предполагать, что величина плотности в пределах каждого частичного отрезка меняется незначительно и приближенно равна r(x_i). Тогда на каждом отрезке разбиения масса участка стержня приближенно равна m_i »r(x_i)Dl_i, а масса всего стержня 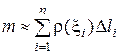и это равенство тем точнее, чем меньше Dl_i (т.е. чем больше п). Поэтому естественно считать искомую массу равной

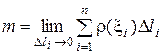
Задача 2. Найти площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми х = а и х = b и отрезком [a, b] оси ОХ.(рис .1).

Решение. Разобьем отрезок [a, b] на п произвольных частей точками х₁, х₂,..., х­_п, обозначим Dх_i длину частичного отрезке [x_i–1, x_i].

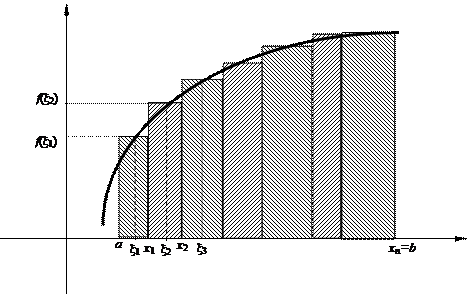
Построим прямоугольники с основаниями Dх_i и высотами f(x_i), где x_i – произвольная точка из отрезка [x_i–1, x_i]. Тогда сумма площадей этих прямоугольников приближенно равна площади заданной криволинейной трапеции

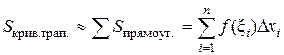
причем это приближенное равенство тем точнее, чем меньше Dх_i .Поэтому можно считать, что .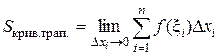

Если сравнить ответы в этих задачах, можно заметить , что в каждом из них содержатся выражения одинакового характера: предел суммы произведений значений заданной функции в точках отрезков разбиения на длины этих отрезков. Оказывается, существует множество других задач, совершенно различного содержания и из различных областей науки, которые приводят к пределам подобного рода. Поэтому естественно рассмотреть соответствующую абстрактную конструкцию .

Определение и свойства ОИ.

Пусть функция y = f(x) определена и непрерывна на отрезке [a, b]. Разобьем отрезок [a, b] на п произвольных частичных отрезков точками

а = х₀ <x₁ < x₂ < ... <x_n = b.

Эти точки называются точками разбиения. Обозначим длину отрезка [x_i–1, x_i] разбиения символом Dх_i , т.е. Dх_i = x_i – x_i–1, а наибольшую из этих длин обозначим l_п ,т.е. l_п = 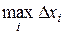. На каждом из частичных отрезков [x_i–1, x_i] возьмем произвольную точку x_i и вычислим значение функции в этой точке f(x_i). Составим сумму 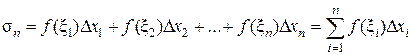, которую называют интегральной суммой для функции f(х), соответствующей данному разбиению и данному выбору точек x_i. Если при п ® ¥ l_п ® 0, то соответствующую последовательность разбиений называют нормальной.

Определение 19.1. Если для всякой нормальной последовательности разбиений существует конечный предел интегральной суммы при l_п ® 0, не зависящий ни от способа разбиения, ни от выбора точек x_i, то это предел называют определенным интегралом от функции f(х) на отрезке [a, b] и обозначают .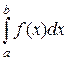

Здесь f(х) – подынтегральная функция, f(х)dx – подынтегральное выражение, х – переменная интегрирования, [a, b] – отрезок интегрирования, a, b – пределы интегрирования: a – нижний, b– верхний.

Таким образом, по определению 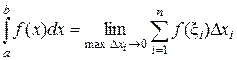. В этом случае функция f(х) называется интегрируемой на отрезке [a, b].

Из определения следует, что определенный интеграл есть число. это число зависит только от вида функции f(х) и от чисел a и b, и не зависит от переменной интегрирования, т.е. = = =... .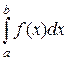

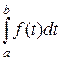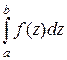Учитывая рассмотренные ранее задачи о массе и о площади криволинейной трапеции, можно дать следующую физическую и геометрическую интерпретацию понятию определенного интеграла:

с физической точки зрения интеграл 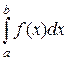численно равен массе прямолинейного тонкого неоднородного стержня длины l = b – a, с переменной линейной плотностью r = f(x), f(x) ³ 0, где х – расстояние от точки стержня до его левого конца;

с геометрический точки зрения интеграл 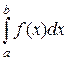численно равен площади криволинейной трапеции, ограниченной графиком функции у = f(x), f(x) ³ 0, прямыми х = а и х = b и отрезком [a, b] оси ОХ .

Мы назвали функцию интегрируемой на отрезке [a, b], если для нее существует определенный интеграл на этом отрезке. Рассмотрим условия интегрируемости функции.

Теорема 19.1.(необходимое условие интегрируемости)

Если функция f(x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.

Заметим, что обратное утверждение не верно, например, функция Дирихле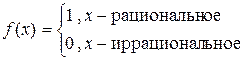

ограничена на любом отрезке [a, b], но не интегрируема на нем, т.к. предел интегральной суммы зависит от выбора точек x_i.

Теорема 19.2.(достаточные условия интегрируемости)

1) Если функция непрерывна на [a, b], то она интегрируема на этом отрезке.

2) Если функция ограничена на [a, b] и имеет на нем лишь конечное число точек разрыва (кусочно-непрерывная функция), то она интегрируема на этом отрезке.

3) Монотонная ограниченная на [a, b] функция интегрируема на этом отрезке.