Нахождение графического и численного решения системы нелинейных уравнений.
Задание. Используя средства MS Excel локализовать графически и уточнить численно решение системы уравнений (1) в заданном интервале независимой переменной x [-1;1]
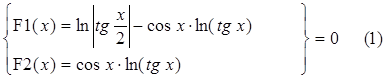 |
Порядок выполнения задания.
1. На листе Лаб3.4 файла Лаб3.xls создаём таблицу (табл.1) значений функций F1(x) , F2(x) и разности значений этих функций F3(x)= F1(x) - F2(x) (рис. 1).

Рис. 1.
2. Присваиваем интервалам клеток имена переменных, значения которых в этих клетках размещены (рис. 2).
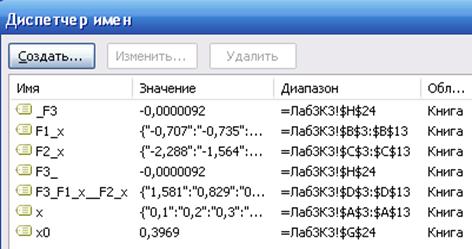
Рис. 2.
3. На основе данных (табл. 1) строим графики функций F1(x) , F2(x) и функции F3(x) = F1(x) - F2(x). Из рисунка (рис. 3) видно, что график функции F3(x) пересекает ось абцисс в точке х≈0,4.Координата точки пересечения графика функции F3(x) c осью абцисс х≈0,4есть приближенное значение корня уравнения F3(x) =0. Из рис.3 также видно, что х≈0,4является также координатой х точки пересечения графиков функций F1(x)иF2(x)и, соответственно, является координатой решения системы уравнений {F1(x); F2(x)}=0по оси абцисс.

Рис. 3.
Для численного решения уравнения F3(x)=0 c применением процедуры Данные, Что - если, Подбор параметра,создаем таблицу 2. (рис. 4).

Рис. 4.
В рассматриваемом примере Таблица 2 располагается в клетках f21:h24.
Присвоим клетке g24 имя x0 (рис. 2) и занесём в неё число 0,40, а в клетку h24 введём формулу:
=LN(ABS(TAN(х0/2)))-COS(х0)*LN(TAN(х0))-COS(х0)*LN(TAN(х0))
Выделив мышкой клеткуh24,выполняем команду
Данные, Анализ что - если, Подбор параметра,Установить в ячейке: h24,Значение:0,Изменяя значение ячейки:h24, Ok.
В результате в клеткеh24компьютер отобразит численное решение уравненияF3(x0)=0и, соответственно, численное значение координаты х решения системы уравнений {F1(x); F2(x)}=0.
Индивидуальные задания к работе 3.4.
Индивидуальное задание должно быть выполнено в отдельном файле с именем Лаб3.xls, на листе Лаб3.4.
Задание. Используя средства MS Excel локализовать графически и уточнить численно решение системы уравнений (2) в заданном интервале независимой переменной x [а;b], табл.3.
 |
Порядок выполнения работы.
1. Вначале, для удобства, на этот же лист Лаб3.4. нужно скопировать условие вашего варианта задания (табл. 3) представив систему уравнений в виде (2).
2. Постройте на этом листе таблицы и диаграммы с графиками функций f 1(x) ,f 2(x)иf 3(x)= f 1(x)-f 2(x)в заданном интервале x [а;b] (их частично можно скопировать из листа Лаб3.1и доработать).
3. Определите (локализуйте) на графиках приближенное решение системы уравнений (2).
4.Уточните приближенное решение системы уравнений и найдите численное решение, используя процедуру Анализ что - если, Подбор параметра.
Таблица 3 - Варианты индивидуальных заданий
| f 1(x) |  | f 2(x) | |
| +1 | 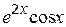 | 1; 1,7 | 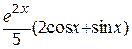 |
| +2 | 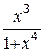 | 1; 1,8 | 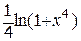 |
| +3 | 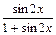 | -0.2; 0.7 |  |
| +4 | 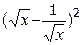 | 4;5.2 |  |
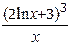 | 1.2; 2 | 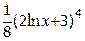 | |
| +6 | 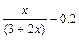 | 1.5; 2.2 | 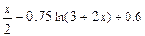 |
| +7 |  | 0.1; 1.1 | 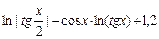 |
| +8 | 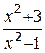 | 2.2; 3.4 |  |
| +9 |  | 0.1; 0.9 | 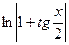 |
 | 4.6; 5.9 | 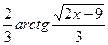 | |
 | 1.2; 2.8 | 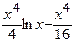 | |
| +12 | 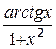 | 0.1; 1.6 | 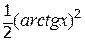 |
| +13 |  | 0.3; 1.2 | 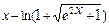 +1 +1 |
 | 0.5; 1.7 | 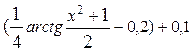 | |
| +15 | 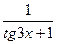 | 0.1; 0.5 | 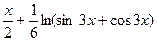 |
| +16 |  | 1.8; 3,4 | 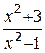 |
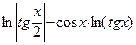 | 0.1; 1.1 | 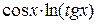 | |
| +18 | 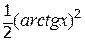 | -0.1; 1.4 | 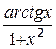 |
| +19 | 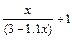 | 1.1; 2.2 | 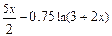 |
| +20 |  | 1.2; 2.8 |  +2 +2 |
| +21 |  | 0; 1 | 1+ 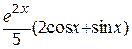 |
| +22 |  | 1.2; 2 | 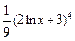 |
| +23 |  | 4.5; 4,55 | 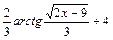 |
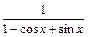 | 0.1; 0.9 | 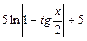 | |
1+  | 1.1; 2.8 | 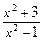 +2 +2 | |
| +26 | X+ 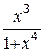 | 1; 3 |  +x +x |
| +27 |  | 0;0.9 |  |
 | 4.0;7.1 | 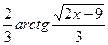 | |
| +29 | 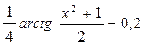 | 1.2;2.8 |  |
 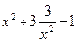 | 1.0;2.0 |  | |
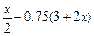 | 1.1;2.2 | 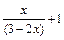 | |
 | 0; 0.9 | 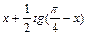 | |
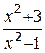 | 1.2;2.8 |  |
