Корреляционное отношение показывает, насколько принятое уравнение регрессии соответствует реальной статистической картине.

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПО ЗЕМЛЕУСТРОЙСТВУ

КАФЕДРА ЗЕМЛЕУСТРОЙСТВА

ЭКОНОМИКО-МЕТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИРОВАНИЕ

ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ

Задания для выполнения лабораторных работ

Для студентов высших учебных заведений по специальностям:

Землеустройство

Земельный кадастр

Городской кадастр

и направлению:

Землеустройство и земельный кадастр

Москва - 2003

УДК 332.3:519.86

Подготовлены к печати кафедрой землеустройства Государственного университета по землеустройству (протокол № от 2003г)

Составители: проф. С.Н.Волков

доц. В.В.Бугаевская

Рецензенты:

ЗАДАНИЕ I

ИСПОЛЬЗОВАНИЕ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ ПРИ РЕШЕНИИ ЗЕМЛЕУСТРОИТЕЛЬНЫХ ЗАДАЧ

Демонстрационная задача №1

При составлении задания на проектирование необходимо установить планируемую урожайность гречихи на расчетный 2010 год. По данным годовых отчетов имеется следующая фактическая урожайность гречихи (ц/га), представленная в таблице 1:

Таблица 1

Исходные данные к задаче 1

Годы	Порядковый номер года, (хj)	Фактическая урожайность, ц/га, (уj)
		8,8
		9,0
		10,4
		11,5
		11,0
		11,8
		12,0
		12,5
		13,0
		13,3
		13,5
		14,2

Необходимо установить имеется ли зависимость между значением урожайности гречихи и годами.

Решение задачи.

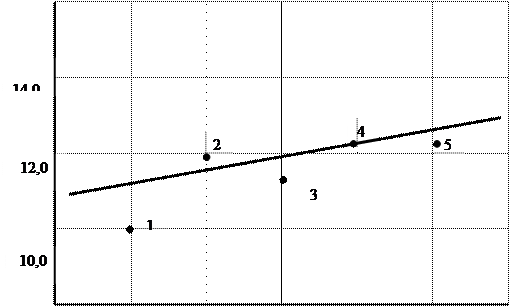
Для того чтобы понять имеется ли зависимость между значением урожайности и годами, построим график в двухмерной системе координат (x,y), где у – урожайность гречихи, х – годы (рис.1).

Графический способ представления исходной информации используется, когда важно не только значение производственного результата, но и направление и характер его изменения.

По графическому представлению (рис. 1), построенному по данным таблицы 1, можно предположить, что зависимость урожайности гречихи от времени носит линейный характер, тогда реальную зависимость можно заменить функциональной линейной связью: y=a₀+a₁x .

Для определения параметров a₀ и a₁ используем принцип наименьших квадратов.

8,0

0 2 4 6 8 10

Рис. 1. Графическое представление зависимости урожайности от времени. Точками показаны результаты наблюдений.

Для получения системы нормальных уравнений приравняем нулю первые производные суммы квадратов отклонений случайных величин (у^j) от соответствующих значений уравнения регрессий 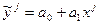по параметрам а₀ и а₁:

;

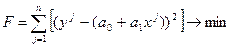
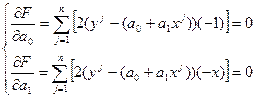Получаем следующую систему нормальных уравнений:

;

;

.

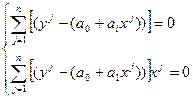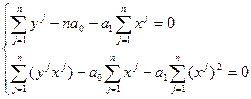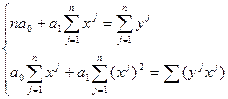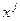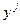В данных уравнениях величины и - статистические данные, представленные в табл.1, а параметры a₀ и a₁ неизвестные величины, которые определим из решения двух уравнений с двумя неизвестными.

Для расчета коэффициентов системы нормальных уравнений а₀, а₁ составим таблицу 2.

Таблица 2

Расчёт коэффициентов системы нормальных уравнений

для расчета параметров «a₀» и «а₁» (случай линейного представления зависимости)

Годы (j)	хj	уj	(хj)2	хj уj	Ўj силаж Ўj=f(x)	(уj)2для расчёта rуx
		8,8		8,8	9,22	77,44
		9,0		18,0	9,68
		10,4		31,2	10,14	108,16
		11,5			10,60	132,25
		11,0			11,06
		11,8		70,8	11,52	139,24
		12,0		84,0	11,98
		12,6		100,0	12,44	156,25
		13,0			12,9
		13,3			13,36	176,89
		13,5		148,5	13,82	182,25
		14,2		170,4	14,28	201,64
∑				982,7		1689,1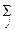2
( )2
∑/п		11,75

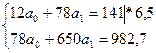
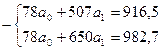
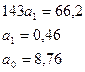
Таким образом линейное функциональное представление зависимости урожайности гречихи от времени примет вид:

ў=f(x)=8,76+0,46х

Подставляя в полученное уравнение значения (х^j), определим расчетную урожайность по годам (ў):

y₉₀=8,76+0,46∙1=9,22

y₉₁=8,76+0,46∙2=9,68

y₉₂=8,76+0,46∙3=10,14

y₉₃=8,76+0,46∙4=10,60

y₉₄=8,76+0,46∙5=11,06

у₂₀₀₁=8,76+0,46∙12=14,28

у₂₀₁₀=8,76+0,46∙21=18,42

Варианты расчета прогнозируемой урожайности для контроля:

у₂₀₁₀=у₁₉₉₅+0,69 ∙х_{2010 -1995}=11,52+0,46∙15=18,42.

Оценка производственной функции

Вычислим коэффициент корреляции, показывающий, насколько зависимость у^j= 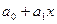^j, выраженная выборкой близка к линейной.

.

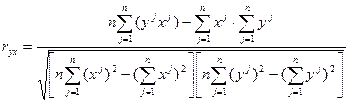Для вычисления коэффициента корреляции воспользуемся расчётами, проведёнными в табл.2.

,

.

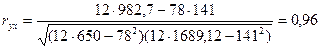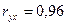Значение коэффициента корреляции говорит о высокой степени линейной корреляции величинуих.

Тесноту нелинейных связей характеризуют выборочным корреляционным отношениям.

Корреляционное отношение показывает, насколько принятое уравнение регрессии соответствует реальной статистической картине.

Для линейной регрессии

.

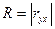Корреляционное отношение определяется по формуле:

.

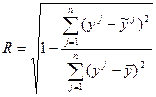Таблица 3

Таблица для расчёта корреляционного отношения (R) и дисперсии

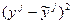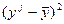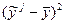	0,18	8,70	6,40
	0,46	7,56	4,28
	0,07	1,82	2,59
	0,81	0,06	1,32
	0,004	0,56	0,48
	0,08	0,003	0,05
	0,0004	0,06	0,05
	0,0036	0,56	0,48
	0,01	1,56	1,32
	0,004	2,40	2,59
	0,10	3,6	4,28
	0,006	6,003	6,40
∑	1,74	32,34	30,25
	Дост	Добщ	Дрег

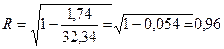
Оценка погрешностей определения коэффициентов корреляции

При малых выборках, когда 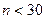стандартная ошибка определения коэффициента парной корреляции вычисляется по формуле:

.

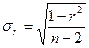Стандартная ошибка определения корреляционного отношения R, вычисляется при 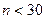по формуле:

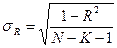, где N – число выборки, K – число факторов.

.

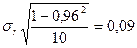Достоверность расчёта коэффициента корреляции высока.

.

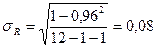Если 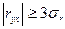, то выборочная оценка коэффициента корреляции приемлема: 0,96 > 0,27 .

В силу линейности регрессии корреляционное отношение не даёт дополнительной информации.

Коэффициент корреляции позволяет сделать вывод о целесообразности использования уравнения регрессии.

Есл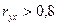и и 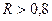, то производственную функцию можно представить в форме линейной регрессии.

Для более полной оценки погрешности необходима оценка закона распределения коэффициентов корреляции.

При малом объёме выборки 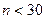и сильной корреляции 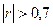закон распределения коэффициента корреляции отличается от нормального, в этом случае используется статистика Фишера.

Доверительный интервал для коэффициента r₀ в генеральной совокупности определится соотношением (случай , ):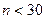

,

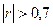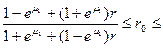
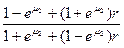где ;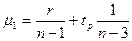

,

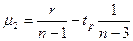t_p – находится с помощью таблиц значений функции Лапласа по уровню доверительной вероятности;

р – уровень доверительной вероятности.

Для ориентировочной оценки доверительных интервалов для r₀ в случае 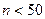, для грубых оценок доверительных интервалов можно использовать, соотношение:

.

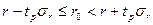Если возьмём уровень доверительной вероятности 80% ( 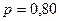), тогда значение 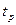из таблицы функции Лапласа будет равно .

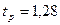Доверительный интервал для коэффициента корреляции определится соотношением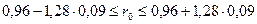

Оценка значимости представления производственной функции или оценка адекватности выбранной сглаженной зависимости 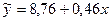реальной стохастической зависимости результата у^j от фактора 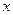^j.

Степень влияния производственного фактора 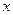^j на результат производства у^j определим на основе дисперсий отклонений сглаженных значений 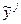от среднего наблюдаемого 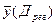и отклонений наблюдаемых величин у^j от сглаженных значений 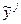, т.е. от линии регрессии (Д_ост).

Дисперсии вычисляются по формулам:

; .

; .

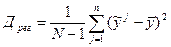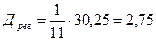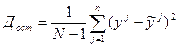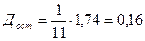Помимо указанных дисперсий вводится их сумма:

; .

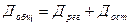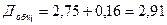Для линейной регрессии:

; .

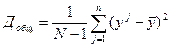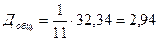Коэффициент детерминации В характеризует какая доля изменений величины у обусловлена изменением фактора х.

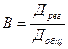, тогда .

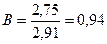Величина (1-В) – характеризует долю изменений величины у от влияния неучтённых факторов. Коэффициент детерминации В=0,94 показывает, что 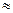90% изменений величины у вызвано изменением производственного фактора х, а (1-В)=1-0,90=0,10, т.е. 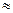10% обусловлены влиянием неучтённых факторов. В случае линейной регрессии ; ; .

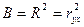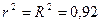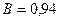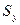- стандартное отклонение у^j от поверхности регрессии.

Выборочная оценка 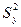дисперсии отклонения случайной величины у^j от линии регрессии 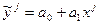равна

;

;

.

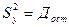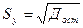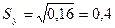Несмещённая выборочная оценка 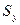стандартного отклонения величины у^j от линии регрессии составляет 0,4, т.е. находится в пределах 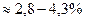от значений величины 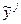, полученных из уравнения регрессии. 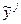изменяется (см.таблица 2) от 9,22 до 14,28, что составляет 4,3 и 2,8%:

9,22 – 100 % 14,28 – 100%

0,4 – х 0,4 –х

х=4,3% х=2,8%.

Проблема достаточности данных

При случае малых выборок необходимо обеспечить выполнения условия:

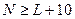, где L – число параметров; т.е. число выборки должно превышать количество параметров хотя бы на 10.

Для нашей задачи минимально необходимый объём выборки 2+10=12.

Экономические характеристики производственных функций

Дополнительный продукт фактора 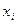(предельная производительность) определяется производной:

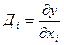(при фиксации всех остальных факторов).

Для линейной зависимости у = a₀+a₁x

,

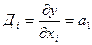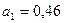
Д_i равен приросту продукции 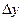за счёт увеличения i-го фактора на единицу 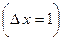и характеризует тем изменения у в данной точке при изменении фактора х_i .

Дополнительный продукт фактора для линейной регрессии есть const, равная 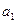.