Метод замены плоскостей проекций
Изменение взаимного положения проецируемой фигуры и плоскостей проекций методом перемены плоскостей проекций, достигается путем замены плоскостей П1 и П2 новыми плоскостями П4 (рис. 4.6). Новые плоскости выбираются перпендикулярно старым. Некоторые преобразования проекций требуют двойной замены плоскостей проекций (рис. 4.7). Последовательный переход от одной системы плоскостей проекций другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.
Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 4.6). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.
Выберем новую плоскость проекций П4, параллельно отрезку АВ и перпендикулярно плоскости П1. Введением новой плоскости, переходим из системы плоскостей П1П2 в систему П1П4 , причем в новой системе плоскостей проекция отрезка А4 В4 будет натуральной величиной отрезка АВ.
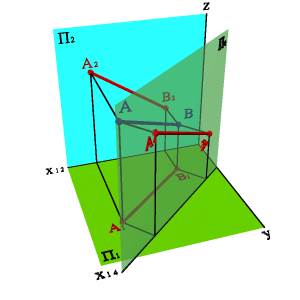
А) модель
Б) эпюр
Рисунок 4.7. Определение расстояния от точки до прямой общего положения методом замены плоскостей проекций
Лекция №5
Плоскость
Плоскость – одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскость обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Некоторые характеристические свойства плоскости:
1. Плоскость есть поверхность, содержащая полностью каждую прямую, соединяющую любые ее точки;
2. Плоскость есть множество точек, равноотстоящих от двух заданных точек.
Плоскость в линейной алгебре - поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением 1-ой степени. Общее уравнение плоскости:
Ax+By+Cz+D=0,
где А, В, С, и D - постоянные, причем А, В и С одновременно не равны нулю.
Способы графического задания плоскостей
Положение плоскости в пространстве можно определить:
1. Тремя точками, не лежащими на одной прямой линии (рис.5.1);
А) модель
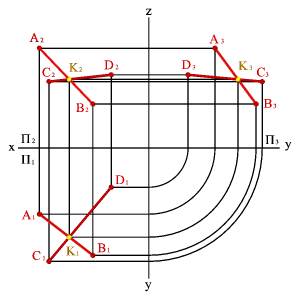
Б) эпюр
Рисунок 5.3. Плоскость заданная двумя пересекающимися прямыми линиями
2. Двумя параллельными прямыми (рис.5.4);
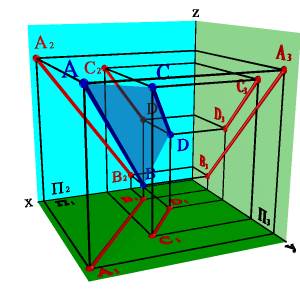
А) модель
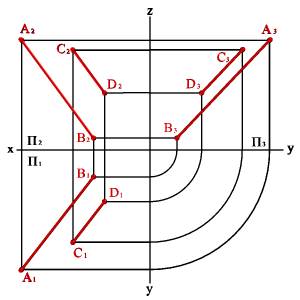
Б) эпюр
Рисунок 5.4. Плоскость заданная двумя параллельными прямыми линиями
О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.5.5).
Следом плоскости называется прямая линия по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный aП1, фронтальный aП2 и профильный aП3 следы.
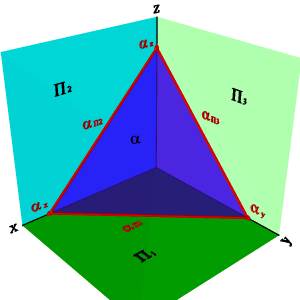
А) модель
Б) эпюр
Рисунок 5.6. Горизонтально проецирующая плоскость
Плоскость перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом aП2 (рис.5.7).
А) модель
Б) эпюр
Рисунок 5.7. Фронтально проецирующая плоскость
Плоскость перпендикулярная профильной плоскости ( a^П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.5.8).
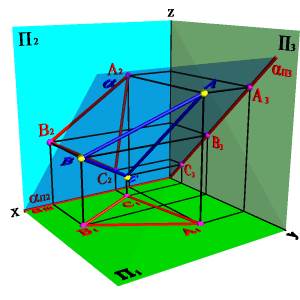
А) модель
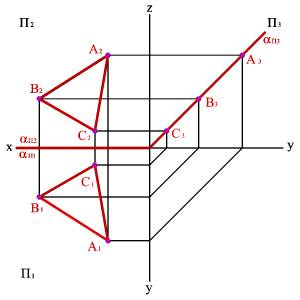
Б) эпюр
Рисунок 5.8. Биссекторная плоскость
Плоскости параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельны исследуемая плоскость, различают:
Горизонтальная плоскость - плоскость параллельная горизонтальной плоскости проекций (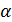 
//П1) - ( 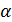^П2,a^П3). Любая фигура в этой плоскости проецируется на плоскость П1 без искажения, а на плоскости П2 и П3 в прямые - следы плоскост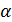и П2 и 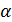П3 (рис.5.9).
А) модель
Б) эпюр
Рисунок 5.10. Фронтальная плоскость
Профильная плоскость - плоскость параллельная профильной плоскости проекций (α//П3), (α^П1, α^П2). Любая фигура в этой плоскости проецируется на плоскость П3 без искажения, а на плоскости П1 и П2 в прямые - следы плоскости α П1 и α П2 (рис.5.11).
А) модель
Б) эпюр
Рисунок 5.11. Профильная плоскость
Следы плоскости
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная, различают:
горизонтальный, фронтальный и профильный следы плоскости.
Каждый след плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой ( как для построения любой прямой). На рисунке 5.12 показано нахождение следов плоскости α(АВС). Фронтальный след плоскости αП2, построен, как прямая соединяющая две точки N(АС) и N(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный след αП1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след αП3 – прямая соединяющая точки (αy и αz) пересечения горизонтального и фронтального следов с осями.
А) модель
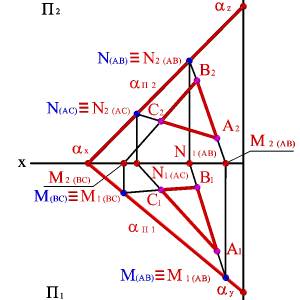
Б) эпюр
Рисунок 5.12. Построение следов плоскости