Провести полное исследование функции
Раздел 1. Линейная алгебра и аналитическая геометрия.
Вариант 1. 1. 
2.Найти миноры и алгебраические дополнения элементов а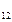 
и а 
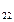матрицы А.
3 4 1
А= 1 -2 0
2 -1 4
3. Написать разложение вектора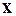 
по векторам 
.
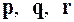x = (2, -1, 4), p = (0, 1, -1), q = (3, -1, 0), r = (4, -1, 2)
4. Найти косинус угла между векторам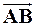и 
и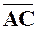 
.
A (1, -2. 3), B (-3, 7, 2), C (3, 1, 4) .
5. Вычислить площадь параллелограмма, построенного на векторах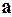 
и 
. 
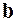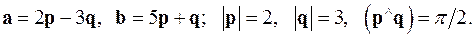
6. Компланарны ли векторы 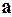, 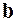и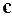 
?
a= (2, 3, 1), b = (1, -1, 3), c = (-1, 9, -11).
Вариант 30.1.
2.Найти миноры и алгебраические дополнения элементов 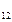а и а 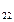матрицы А.
3 -2 4
А= 3 4 -2
2 -1 -1
3. Написать разложение вектора 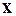по векторам .
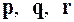x = (3, 1, -5), p = (-1, 1, 0), q = (2, 0, -1), r = (3, 1, 6)
4. Найти косинус угла между векторам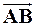и и .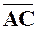
A (4, -1. 6), B (2, 1, -2), C (1, 3, 9) .
5. Вычислить площадь параллелограмма, построенного на векторах 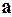и . 
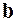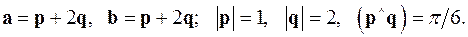
6. Компланарны ли векторы 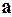, 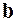и ?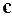
a= (3, -2, 1), b = (2, 1, 2), c = (3, -1, -2).
Вариант 1.2.
Задача 1. Вычислить объем тетраэдра с вершинами в точках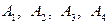 
и его высоту, опущенную из вершины 
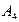на грань 
.
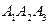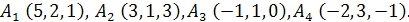
Задача 2. Найти расстояние от точки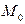 
до плоскости, проходящей через точки 
.
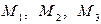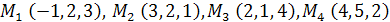
Задача 3. Найти угол между плоскостями.
Задача 4. Написать канонические уравнения прямой.
Задача 5. Найти точку пересечения прямой и плоскости.
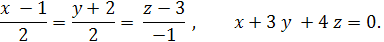
Вариант 30.2.
Задача 1. Вычислить объем тетраэдра с вершинами в точках 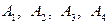и его высоту, опущенную из вершины 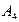на грань .
.
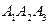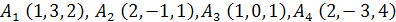Задача 2. Найти расстояние от точки 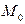до плоскости, проходящей через точки 
.
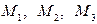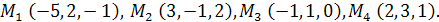
Задача 3. Найти угол между плоскостями.
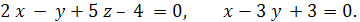
Задача 4. Написать канонические уравнения прямой.
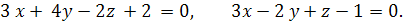
Задача 5. Найти точку пересечения прямой и плоскости.
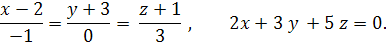
Раздел 2. Введение в математический анализ.
Вариант 1.
1. Найти предел последовательности
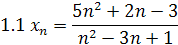
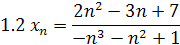
2. Найти предел функции
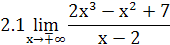
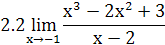
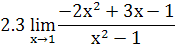
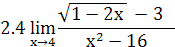
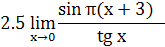
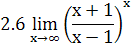
3. Доказать, что функции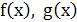 
являются бесконечно малыми одного порядка малости при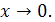 
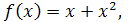
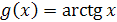
4. Найти предел функции, используя эквивалентные бесконечно малые функции
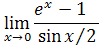
5.Найти область непрерывности функции, точки разрыва, исследовать их характер: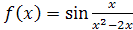 
Вариант 30.
1. Найти предел последовательности
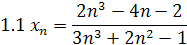
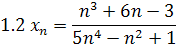
2. Найти предел функции
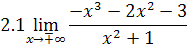
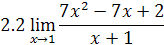
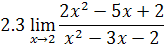
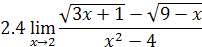
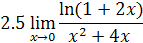
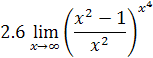
3. Доказать, что функции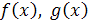 
являются бесконечно малыми одного порядка малости при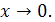
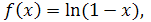
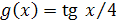
4. Найти предел функции, используя эквивалентные бесконечно малые функции
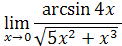
5. Найти область непрерывности функции, точки разрыва, исследовать их характер.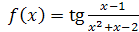 
Раздел 3. Дифференциальное исчисление.
Вариант 1.1.
1.Найти производные указанных порядков явно заданных функций:
а)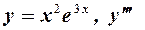 
;
б)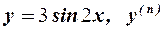 
;
в)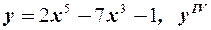 
.
2.Найти производные указанных порядков параметрически заданных функций:
а)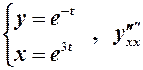 
; б) 
.
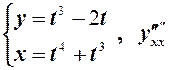3.Найти производные указанных порядков неявно заданных функций:
а)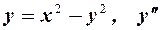 
; б)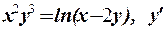 
.
Вариант 30.1.
1.Найти производные указанных порядков явно заданных функций:
а)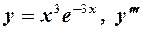 
;
б)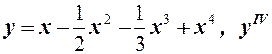 
;
в)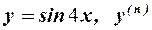 
.
2.Найти производные указанных порядков параметрически заданных функций:
а)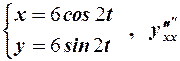 
; б) 
.
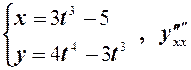3.Найти производные указанных порядков неявно заданных функций:
а)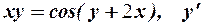 
; б)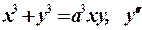 
.
Вариант 1.2.
Провести полное исследование функции
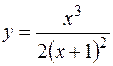
и построить её график.
Вариант 30.2.
Провести полное исследование функции
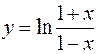
и построить её график.