Исследование системы линейных уравнений

Рассмотрим ступенчатую систему (2.3). Возможны следующие случаи:

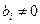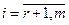1) Если найдется , где , то система (2.3) несовместна.

2) Если 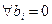, , 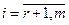то система (2.3) совместна, 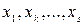- главные неизвестные; остальные неизвестные – свободные.

3) Если в системе (2.3) содержится хотя бы одна свободная неизвестная, то система является неопределенной.

4) Если система (2.3) не содержит свободных неизвестных, то данная система является определенной.

2.4. Арифметическое n-мерное векторное пространство.

Определение и свойства

В связи с системами линейных уравнений нам приходилось рассматривать строки длины n, в которые вкладывался разный смысл. Приведение системы или матрицы к ступенчатому виду включало, помимо элементарного преобразования типа (I) два важных акта: умножение строки на число и сложение двух строк. Те же действия можно производить и с решениями однородной линейной системы. С другой стороны, любая строка, что бы она ни выражала, является элементом «универсального» множества Rⁿ - n-й декартовой степени множества R действительных чисел. Поэтому желательно изучить общий объект, свойства которого автоматически переносились бы на матрицы и на решения однородных систем.

Определение. Упорядоченную совокупность, состоящую из n чисел 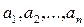будем называть n-мерным вектором.

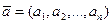- вектор-строка,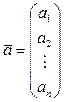 вектор-столбец.

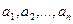- координаты вектора .

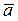Рассмотрим вектор .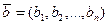

Определение. Два вектора называются равными: 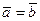, если равны их соответствующие координаты, т.е.

.

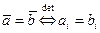
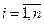Введем операции:

1. Сложение векторов:

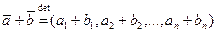
2. Умножение вектора на скаляр:

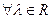
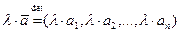
Определение. Множество всех n-мерных векторов с введенными операциями сложения и умножения на скаляр будем называть арифметическим n-мерным векторным пространством .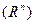

Свойства операций.

Сложение

1⁰ 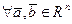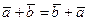- коммутативность

2⁰ 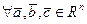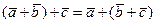- ассоциативность

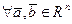
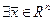
3⁰ 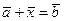- обратимость

1⁰ - 3⁰ - коммутативная группа (или Абелева группа)

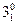
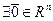
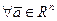
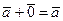
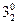
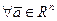
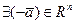
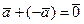
Умножение

4⁰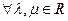

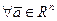
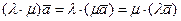
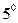
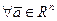
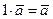
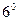
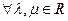
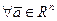
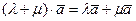
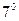
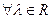
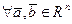
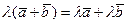
6⁰ и 7⁰ - дистрибутивные законы

Все 7 свойств дают понятие векторного (линейного) пространства

Линейная зависимость и линейная независимость

Конечной системы векторов

Рассмотрим конечную систему векторов .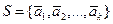

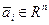
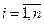Определение. Вектор 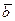будем называть линейной комбинацией конечной системы векторов S, если существует такой набор скаляров 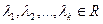, что 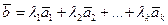. По-другому: вектор 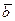линейно выражается через вектора системы S.

Определение. Множество всех комбинаций конечной системы векторов S будем называть линейной оболочкой конечной системы векторов:

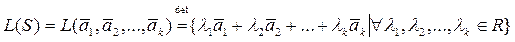
В линейной оболочке операции сложения и умножения на скаляр – замкнуты:

1)

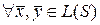
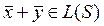
2)

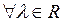
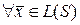
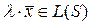
Определение. Конечную систему векторов будем называть линейно зависимой, если найдется такой ненулевой набор скаляров (т.е. хотя бы один скаляр отличен от нуля) 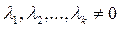, что выполняется равенство (*).

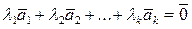В противном случае, т.е. если равенство (*) выполняется только лишь при нулевом наборе скаляров, систему векторов будем называть линейно независимой.

Свойства

1. Всякая конечная система векторов, содержащая нулевой вектор, является линейно зависимой.

Доказательство.

Пусть 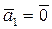. Докажем, что 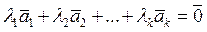при ненулевом наборе скаляров 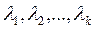. Пусть, например, 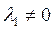, 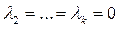. Тогда

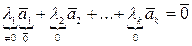
Нашелся такой ненулевой набор скаляров, что выполняется равенство (*). Свойство доказано.

2. Если подсистема конечной системы векторов линейно зависима, то сама система линейно зависима.

Доказательство.

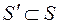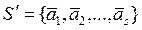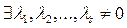
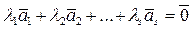
Пусть , -линейно зависима. По определению, 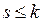. Тогда

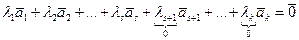
Нашелся ненулевой набор скаляров 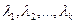, следовательно, сама система S – линейно зависима.

3. Любая подсистема данной системы является линейно независимой, если сама система линейно независима.

Доказательство.

Проведем его методом от противного. Предположим, что 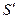-линейно зависима, тогда по 2 свойству S тоже линейно зависима. А это противоречит условию, значит наше предположение неверно и 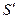-линейно независима.

4. S – линейно зависима тогда и только тогда, когда существует вектор системы S, который линейно выражается через остальные векторы этой системы: .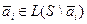

Доказательство.

Пусть S – линейно зависима, т.е. 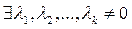, что выполняется равенство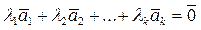

Не ограничивая общности, будем считать, что 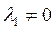. Тогда

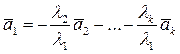
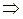
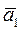- линейная комбинация остальных векторов.

Наоборот, пусть 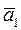является линейной комбинацией остальных векторов: 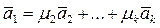. Тогда 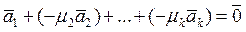- нашелся искомый ненулевой набор скаляров, т.е. система S является линейно зависимой.

5. S – линейно независима тогда и только тогда, когда

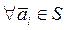
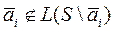
6. Любая конечная система векторов, содержащая число векторов больше чем n, является линейно зависимой.

Доказательство.

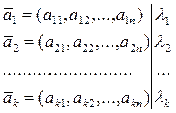
Составим линейную комбинацию этих векторов и приравняем к .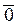

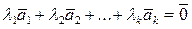
Распишем по координатам:

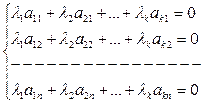
k>n (число неизвестных больше числа уравнений), поэтому 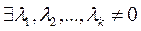что выполняется равенство 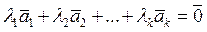, т.е. система S является линейно зависимой.