Дәріс. Фигура кескіннің анықтамасы және оған қойылатын талаптар. Жазық фигураларды кескіндеу.

Анықтама: Фигураның кескіні деп оның параллель проекциясына ұқсас фигураны айтамыз.

Геометриялық есептерді шығару барысында қолданылатын фигура кескіндері еркін параллель проекциялау негізінде салынады. Яғни, берілген фигураның проекция жазықтығына қатысты орналасуы мен проекция бағыты анықталмайды. Стереометрияда әртүрлі жазықтықтарда жатқан жазық фигуралардың бәрін бір сызба жазықтығына кескіндеуге тура келеді. Мысалы, параллелепипедті кескіндеу кезінде, оның алты түрлі жазықтықтарда жатқан жақтарын (параллелограмдарды) бір жазықтыққа кескіндейміз.

Олай болса, кеңістік фигурасын кескіндеу үшін, біріншіден, жазық фигураларды кескіндеу мәселесіне тоқталу керек. Параллель проекциялау әдісін пайдаланып кескіндеу барысында, берілген фигура жазықтығы мен бейнелеу жазықтығы параллель болмаса, онда жазық фигура кескіндеу кезінде өзгеріске ұшырайтыны түсінікті.

Жазық фигураларды кескіндеу теориясы мынадай екі теоремаға негізделген.

Теорема-1 (Бар болудың бірінші теоремасы). Берілген қандай да болмасын үшбұрышты, кез келген үшбұрыш етіп кескіндеуге болады.

Теорема-2. Егер А^/В^/С^/ үшбұрышының кескіні берілген болса, онда осы үшбұрыш жатқан жазықтықтың әрбір нүктесінің кескіні де бір мәнді анықталған болады.

Олай болса, осы теоремалар негізінде тең қабырғалы үшбұрыштың, тең бүйірлі үшбұрыштың және тікбұрышты үшбұрыштың кескіндері кез келген үшбұрыш болатынын көреміз. Сондай-ақ, үшбұрыш жазықтығының әрбір нүктесінің кескіні бірмәнді анықталады. Мысалы, А^/В^/С^/ теңбүйірлі үшбұрышы берілген болсын (А^/С^/=В^/С^/). Осы үшбұрышты және оның С^/Н^/ биіктігін кескіндейік.

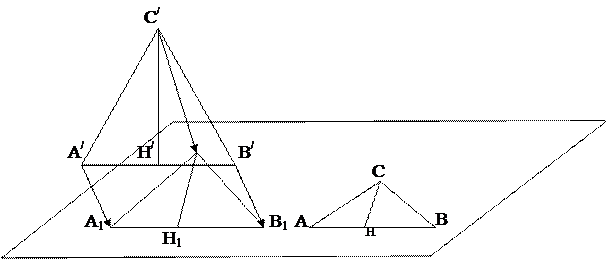
72-сурет. А^/В^/С^/ теңбүйірлі үшбұрышы мен оның С^/Н^/ биіктігін кескіндеу реті.

Шешуі: А^/В^/С^/ үшбұрышының кескіні 1-теоремаға сәйкес кез келген АВС үшбұрышы болады. Ал 2-теоремаға сәйкес А^/В^/С^/ үшбұрышының әрбір нүктесінің кескіні АВС үшбұрышы арқылы бірмәнді анықталады. Демек, осы үшбұрыштың С^/Н^/ биіктігін енді бұлай еркін түрде кескіндей алмаймыз. А^/Н^/=Н^/В^/ болғандықтан және кескіндеу параллель проекциялау негізінде орындалатындығын ескеріп, параллель проекциялаудың 4⁰-қасиетіне сәйкес (параллель проекциялауда, бір түзудің немесе параллель түзулердің бойында жатқан кесінділердің қатынасы сақталады) Н нүктесі АВ қабырғасының ортасы болады (72-сурет).

Осы теоремалар негізінде басқа да жазық фигураларды кескіндеуге тоқталайық.

Мысалы: А^/В^/С^/D^/ параллелограмын кескіндеу керек болсын.

Шешуі: Берілген параллелограмнан А^/В^/С^/ үшбұрышын алып, 1-теорема бойынша оның кескіні АВС үшбұрышын аламыз. Параллелограмның төртінші төбесінің D кескіні параллель проекциялаудың қасиеттері бойынша салынады. Яғни, А^/В^/║С^/D^/ және В^/С^/║А^/D^/ болғандықтан, оған сәйкес АВ║СD, ВС║АD болады. Демек, кез келген параллелограмның кескіні параллелограмм болатындығы шығады.

Олай болса, кез келген көпбұрышты (жазық фигураны) кескіндеу үшін, оның құрылымынан қандай да бір үшбұрыш бөлініп алынып, 1-теорема негізінде кескінделіп, ал басқа төбелерінің кескіндері параллель проекциялаудың қасиеттері негізінде салынады екен. Сонда кескіндеу кезінде, жазық фигура құрамынан таңдалып алынған үшбұрыштың төбелері базистік нүктелер деп аталады.

Бұдан мынадай қорытындылар жасаймыз: Үшбұрыштың кескіні – кез келген үшбұрыш, параллелограмның, тіктөртбұрыштың, ромбының және квадраттың кескіндері – параллелограмм, ал трапецияның кескіні табандарының қатынасы сақталатын трапеция болады. Сондай-ақ, дұрыс бесбұрыштың кескіні – кез келген бесбұрыш, дұрыс алтыбұрыштың кескіні – кез келген алтыбұрыш т.с.с. Ал шеңбердің кескіні – эллипс.