Установка параметров моделирования и сохранение модели

Перед выполнением моделирования в панели управления меню Simulation окна моделирования необходимо предварительно задать параметры.

- Задать интервалы моделирования (Simulation time). Начальное время (Start time), как правило, задается равным нулю, величина конечного времени (Stop time) задается пользователем; по условиям задачи в нашем случае достаточно задать, например, равным 10.

- В параметрах обмена с рабочей областью на вкладке Workspace I/O \Save to Workspace переменную Timeдля удобстваизменим со значения tout (по умолчанию) на t, а переменную Output со значения yout (по умолчанию) на z (сохраняемая ошибка регулирования).

- Сохраним модель по командеSave Asс расширением .mdl.Пусть имя модели для определенности будет“Lab5 ”(в соответствии с номером данной лабораторной работы).

Представление результатов имитационного моделирования

Для представления результатов целесообразно руководствоваться следующим алгоритмом - процедурой.

- Формировать исходный массив Z из значений ошибок регулирования z в каждой реализации.

- Для получения числовых характеристик случайной величины z (математического ожидания и среднеквадратического отклонения - СКО) можно использовать функции meanи std соответственно: mean(Z), std(Z), где Z – массив, сформированный по результатам цикла моделирования, состоящего из заданного количества реализаций N. (Чем большеN, тем выше достоверность получаемых числовых характеристик случайной величины).

- Для наглядного представления ошибки z в каждой реализации моделирования удобно воспользоваться специальной графикой (plot без указания аргумента строящейся функции). В этом случае в качестве аргумента система принимает номер элемента вектора ошибки (в нашем случае – номер реализации). Оператор должен иметь вид: plot(Z).

- Еще более наглядным является представление вектора в виде столбчатой диаграммы с помощью функции bar: bar(z).

- Еще одна полезная инженеру функция – hist (построение графика гистограммы заданного вектора).Стандартное обращение к ней имеет вид: hist(Z, z),где Z– вектор, гистограмму которого нужно построить; z –вектор, определяющий интервалы изменения первого вектора Z.

Для организации приведенной процедуры необходимо создать программу в среде Matlab.

В языке Matlab имеются программы двух типов: так называемые Script-файлы (файлы-сценарии или управляющие программы) и файл-функции (процедуры). Все программы должны иметь расширение имен файлов .m.

Создание программы осуществляется при помощи текстового редактора, вызываемого по команде File Þ New Þ M-file. Пусть имя файла для определенности будет“Lab5_1 ”

М-файл (Script-файл), реализующий представленный выше алгоритм, может иметь следующий вид.

w=1% начальное значение переменой w источника случайного сигнала, формирующего шум S1

v=2% начальное значение переменой v источника случайного сигнала, формирующего помеху S2

N=50% количество реализаций случайного процесса

Z(N)=0% формирование массива ошибок и задание начальных значений массива

for(i=1:N) % формирование цикла из N реализаций

w=w+1

v=v+1

Lab5 % вызов файла "Lab5.mdl" для изображения на экране

sim('Lab5') % запуск файла "Lab5.mdl" на моделирование

Z(i)=z % формирование массива случайной величины (контролируемого сигнала ошибки)

end % завершение цикла

Mz=mean(Z) % вычисление среднего значения ошибки

sigz=std(Z) % вычисление среднеквадратического отклонения ошибки

%plot(Z),grid % графическое изображение значений ошибки по реализациям

%bar(Z),grid % изображение значений сигнала в реализациях в виде столбчатой диаграммы

z=[-2:0.2:2] % задание интервала изменения сигнала ошибки для построения гистограммы

hist(Z,z),grid % построение графика гистограммы

Результаты моделирования

Приведем результаты моделирования для случая N = 100.

Mz = 0.3145; sigz = 0.8465 -числовые оценки случайного процесса z: соответственно среднее значение и среднеквадратическое отклонение ошибки регулирования.

Графические изображения значений ошибки по реализациям приведены на рисунке 3 (с использованием функции plot(Z)),на рисунке 4 (в виде столбчатой диаграммы bar(Z)). А на рисунке 5 приведена гистограмма результата моделирования, полученная по функции hist(Z,z).

Задание на самостоятельную работу

Исходная схема

Имеется нестационарная и нелинейная система, структурная схема которой представлена на рисунке 6,

где x, y– вход и выход системы; W_i (s) – операторные выражения передаточных функций системы; z – ошибка регулирования; N – нелинейное звено; S₁- шум сигнала на входе; S₂ - случайная помеха в составе ошибки регулирования.

Исходные параметры системы для различных вариантов заданы в таблицах 1 и 2.

Требования к работе

5.3.2.1. “Набрать ” модель с использованием пакета SIMULINK.

Таблица 1. Характеристики объекта управления

t, c
KОУ, м/с
fОУ,Гц	1.0	4.2	5.0	4.0	2.7	2.3	1.8

Характеристики динамических звеньев определяются следующими выражениями:

· Корректирующее звено:

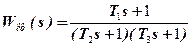, (1)

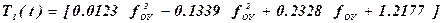где , (2)

а f_ОУ (t) – из таблицы 1, T₂ иT₃ - из таблицы 2.

· Переменное усилительное звено:

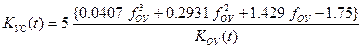, (3)

где K_ОУ(t), f_ОУ (t) – известные зависимости из таблицы 1.

· “Нестационарный” объект управления:

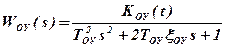, (4)

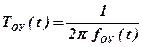где ,(5)

а K_ОУ(t) – из таблицы 1, x_ОУ – из таблицы 2.

· Кинематическое звено

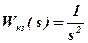. (6)

· Нелинейное звено N – одним из двух видов

- первый,определяемый зависимостью

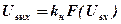, (7)

где 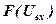- нелинейность типа насыщение с порогами ограничения на уровне ±1;

k_н – коэффициент передачи до ограничения сигнала, k_н = 0.20;

- второй,определяемый зависимостью

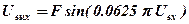, (8)

где 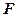- нелинейность типа ”насыщение” с порогами ограничения на уровне ±8,ограничивающий входной сигналU_вх.

Рекомендация: При формировании нелинейности второго типа воспользуйтесь блоком Trigonometric Function из раздела блоков Math Operations.

Характеристики шумов:

Закон распределения	Нормальный	Равномерный
Характеристики законов	Среднее значение	Дисперсия	Минимальное значение	Максимальное значение
M	D	min	max

5.3.2.2. Провести исследование системы при задании на вход гармонического сигнала x=A_вхsin (2π f_вх t) при двух значениях частоты: f_вх=0.5 Гц и f_вх=1 Гц с переменной амплитудой A_вх=A₀+ct, где A₀ – начальное значение амплитуды, c - скорость изменения амплитуды.

Рекомендация. При формировании переменой амплитуды A_вх воспользуйтесь источником линейно изменяющегося сигнала - блоком Ramp -из раздела Sourcesбиблиотеки SIMULINK

· В процессе моделирования оценить сходимость результатов, варьируя количеством реализаций N = [50, 100, 300, 500] по величинам среднего значения ошибки M(z) и среднеквадратического отклонения Sig(z) в каждой серии из N реализаций.

· Представить соответствующие графики распределения ошибки z в реализациях.

· Для наглядности анализа результаты свести в таблицу приведенного ниже образца.

Таблица. Образец таблицы с результатами моделирования

Количество реализаций N	Среднее значение M(z)	Среднеквадратическое отклонение Sig(z)	График plot (Z) с распределением ошибки в каждой реализации	График гистограммы вектора Z во всем интервале изменения ошибки z в течение цикла из N реализаций hist (Z, z)
fвх=0.5 Гц
			Рисунок 1.1	Рисунок 1.2
			Рисунок 1.3	Рисунок 1.4
			Рисунок 1.5	Рисунок 1.6
			Рисунок 1.7	Рисунок 1.8
fвх=1 Гц
			Рисунок 2.1	Рисунок 2.2
			Рисунок 2.3	Рисунок 2.4
			Рисунок 2.5	Рисунок 2.6
			Рисунок 2.7	Рисунок 2.8

Отчетность

1). Результаты исследований сохранять в личной папке в соответствующих файлах с расширениями .m (Script-file) и .mdl (Model).

2). По работе оформить отчет в виде Пояснительной записки в текстовом процессоре MS Word:

- на электронном носителе;

- на бумажном носителе.

Таблица 2. Исходные данные для моделирования по вариантам

№ варианта	Входной сигнал Aвх	Фильтр Wкф(s)	Kус(t)	N,в соответствии с выражением	Объект управления WОУ(s)	Шумы
A0	c	T1, с,	T2, с	T3, с	KОУ(t)	TОУ, с,	ξОУ	S1	S2
закон	закон	закон	закон
нормальный	параметры	равномерный	параметры	нормальный	параметры	равномерный	параметры
M	D	min	max	M	D	min	max
	0.30	0.05	в соответствии с выражением (2) и таблицей 1	0.04	0.005	в соответствии с выражением (3) и таблицей 1	(34)	В соответствии с таблицей 1	в соответствии с выражением (5) и таблицей 1	0.4	да		0.2	-	-	да	-0.2	0.2
	0.45	0.05	0.05	0.005	(35)	0.3	-	да	-0.3	0.3	да		0.2	-
	0.55	0.04	0.06	0.005	(34)	0.2	да	0.2	0.2	-	-	да	-0.3	0.3
	0.30	0.04	0.07	0.005	(35)	0.6	да	0.2	0.3	-	да	0.1	0.2	-
	0.45	0.03	0.08	0.005	(34)	0.6	-	да	-0.4	0.4	да	0.2	0.3	-
	0.55	0.02	0.09	0.005	(35)	0.5	да	0.1	0.6	-	-	да	-0.4	0.4
	0.65	0.01	0.10	0.005	(34)	0.4	-	да	-0.5	0.5	да	0.1	0.2	-
	0.75	0.01	0.04	0.005	(35)	0.3	да	0.2	0.2	-	-	да	-0.3	0.3
	0.85	0.01	0.05	0.004	(34)	0.2	-	да	-0.6	0.6	да		0.2	-
	0.90	0.01	0.06	0.003	(35)	0.1	да	0.3	0.3	-	да		0.2	-
	1.00	0.01	0.07	0.004	(34)	0.4	-	да	-0.4	0.4	-	да	-0.5	0.5
	1.20	0.01	0.08	0.007	(35)	0.3	да	0.1	0.5		да		0.2	-
	0.30	0.05	0.09	0.009	(34)	0.2	-	да	-0.3	0.3	-	да	-0.3	0.3
	0.45	0.04	0.10	0.010	(35)	0.6	да	0.2	0.3	-	да	-0.1	0.2	-
	0.55	0.03	0.04	0.004	(34)	0.6	-	да	-0.2	0.2		да	-0.4	0.4
	0.30	0.05	0.05	0.003	(35)	0.5	да	0.3	0.3	-	да	-0.2	0.2	-
	0.45	0.04	0.06	0.004	(34)	0.4	-	да	-0.3	0.3	-	да	-0.3	0.3
	0.55	0.03	0.07	0.007	(35)	0.3	да	0.1	0.4	-	да	-0.1	0.3	-
	0.65	0.02	0.08	0.009	(34)	0.2	-	да	-0.4	0.4	-	да	-0.2	0.2
	0.75	0.02	0.09	0.010	(35)	0.1	да	0.2	0.3	-	да	0.2	0.2	-
	0.85	0.01	0.10	0.004	(34)	0.3	-	да	-0.2	0.2	-	да	-0.1	0.1
	0.90	0.01	0.04	0.003	(35)	0.2	да	0.3	0.3	-	да	0.1	0.4	-
	1.00	0.01	0.05	0.004	(34)	0.1	-	да	-0.3	0.3	-	да	-0.3	0.3
	1.20	0.01	0.06	0.007	(35)	0.2	да	0.2	0.3	-	да	0.1	0.2	-

Использованные источники

1. Вентцель Е.С. Теория вероятностей: Учебник для вузов – М.: Высшая школа. 1999. – 576 с.

2. Гультяев А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие – Санкт-Петербург: Корона, 1999. – 286 с.

3. Егоренков Д.Л., Фрадков А.Л., Харламов В.Ю. Основы математического моделирования. Построение и анализ моделей с примерами на языке MatLab – Санкт-Петербург: БГТУ “Военмех”, 1996. – 188 с.

4. Земсков А.В. Теория, конструкция и основы проектирования систем управления. Раздел 1. Теория автоматического управления. - МО РФ: Михайловская военная артиллерийская академия, 2005. – 312 с.

5. Лазарев Ю.Ф. MatLAB 5.x. – К: Издательская группа BHV, 2000. – 384 с.

6. Макаров И.М., Менский Б.М. Линейные автоматические системы (элементы теории, методы расчета и справочный материал). – М.: Машиностроение, 1982. – 504 с.

7. Медведев В.С., Потемкин В.Г. Control Sistem Toolbox. Matlab 5 для студентов. – М: Диалог МИФИ, 1999. – 456 с.

8. Методы классической и современной теории автоматического управления: Учебник в 5-ти томах; Т.1: Математические модели, динамические характеристики и анализ систем управления / Под ред. К.А. Пупкова, Н.Д. Егупова. – М: Издательство МГТУ им. Н.Э. Баумана, 2004. – 656 с.

9. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. Перевод с английского. – М: Мир, 1978. – 848 с.

10. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. – М.: ФИЗМАТЛИТ, 2002. – 320 с.

11. Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. для вузов по специальности “Автоматизир. системы обработки информ. и упр.” – М: Высшая школа, 1998. – 319 с.: ил.

12. Сольницев Р.И. Автоматизация проектирования систем автоматического управления: Учеб. для вузов по специальности “Автоматика и управление в технических системах” – М: Высшая школа, 1991. – 335 с. : ил.

13. Черных И.В. SIMULINK: среда создания инженерных приложений / Под общ. Ред. к.т.н. В.Г. Потемкина. – М.: ДИАЛОГ-МИФИ. 2003. – 496 с.