Течение совершенного газа через недеформируемый пласт
В данных условиях k=const, h=const, по (2.29) -r =rcт р/ рст и, согласно (3.15) 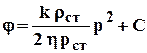 .
.
В данной постановке имеем:
Распределение давления из (3.10)
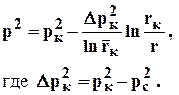 (3.37)
(3.37)
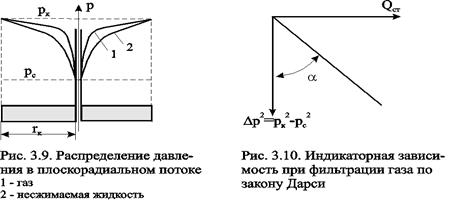
Если сравнить распределения давления в случае потока газа с соответствующим распределением для однородной несжимаемой жидкости (рис. 3.9), то увидим, что для газа давление вблизи стенок скважины изменяется более резко, чем для несжимаемой жидкости. Пьезометрическая кривая для газа имеет, следовательно, более пологий характер на большем своём протяжении, чем кривая несжимаемой жидкости; однако у неё более резкий изгиб у стенки скважины, чем у кривой несжимаемой жидкости.
Уравнение притока
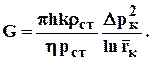 (3.38)
(3.38)
Если обе части уравнения (3.38) разделить наrст , то получим формулу для объёмного дебита, приведенного к стандартному давлению
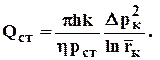 (3.39)
(3.39)
Таким образом, индикаторная зависимость для газа описывает линейную зависимость дебита от разницы квадратов пластового и забойного давлений в отличие от индикаторной зависимости для несжимаемой жидкости, где устанавливается линейная связь дебита с разницей самих значений пластового и забойного давлений.
Распределение градиента давления получим из (3.3) 
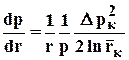 . (3.40)
. (3.40)
Из данной формулы следует, что градиент давления вблизи забоя резко возрастает как за счёт уменьшения r, так и за счёт падения давления р, вызванного сжимаемостью газа.
Изменение скорости фильтрации выведем из (2.7) 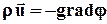 при использовании уравнения состояния (2.29) r =rcт р/ рст
при использовании уравнения состояния (2.29) r =rcт р/ рст
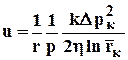 . (3.41)
. (3.41)
Из (3.41) видно, что скорость фильтрации слабо меняется вдали от скважины и резко возрастает в призабойной зоне.
Уравнение индикаторной линии
Уравнение (3.39) устанавливает линейную связь между дебитом и разностью квадратов контурного и забойного давлений, поэтому для простоты исследований индикаторная диаграмма при фильтрации идеального газа по закону Дарси строится в координатах Qст –(рк2-рс2). В этом случае имеем прямую (рис.3.10) , проходящую через начало координат с угловым коэффициентом
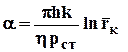 . (3.42)
. (3.42)
Преобразуем данное уравнение с целью анализа вида данной индикаторной зависимости в координатах Qст – (рк - рс). Тогда Qcт=a(рк2 - рс2), но разность квадратов можно представить в виде рк2 - рс2 = 2ркDрс - (Dрс)2, где Dрс= рк - рс. С учётом данного обстоятельства соотношение (3.39) перепишется в виде
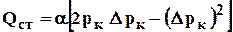 , (3.43)
, (3.43)
Т.о. для случая фильтрации совершенного газа по закону Дарси, имеем параболу с осью, параллельной оси дебитов (рис.3.11). Ветвь параболы, изображенная пунктиром, физического смысла не имеет.
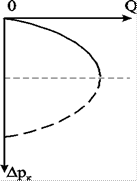 |
Рис. 3.11. Индикаторная зависимость при фильтрации газа
по закону Дарси.
