Решение задач одномерной оптимизации

При решении задачи поиска экстремума (максимума или минимума) функции y=f(x) одной переменной выделяют задачи поиска локального и глобального экстремума. При этом задача нахождения максимума целевой функции сводится к задаче нахождения минимума путем замены функции f(x)на -f(x), поэтому в дальнейшем будем говорить только о поиске минимума функции, то есть такого x*Î[a, b], при котором f(x*) = minf(x).

Интервал, на котором локализован единственный минимум, называется отрезком неопределенности.

Необходимым условием существования экстремума дифференцируемой функции f(x) является выполнение равенства f¢(х) = 0. Точка х, удовлетворяющая данному условию, называется точкой стационарности. Достаточнымусловием существования минимума в точке стационарности является выполнение неравенства f¢¢(х)>0, а максимума - f¢¢(х)<0.

Задача одномерной оптимизации имеет единственное решение в том случае, если функция f(x)на отрезке [a;b] имеет только один экстремум. Тогда говорят, что функция унимодальна на отрезке [a;b].

Достаточнымиусловиями унимодальной функции на отрезке [a;b] являются:

- для дифференцируемой функции f(x) ее производная f¢(х)- неубывающая;

- для дважды дифференцируемой функции f(x) выполняется неравенство f¢¢(х)³0.

Для решения задачи одномерной оптимизации с заданной степенью точности используются методы: дихотомии, золотого сечения, средней точки и многие другие [1]. При этом суть методов одномерного поиска заключается в том, что на каждой итерации интервал неопределенности уменьшается и стягивается к точке минимума. Уменьшение отрезка происходит до тех пор, пока на некоторой n-й итерации отрезок неопределенности [b_n;a_n] не станет соизмеримым с заданной погрешностью e, то есть будет выполняться условие |b_n-a_n| <e. Тогда за точку минимума можно принять любую точку, принадлежащую этому отрезку, в частности, его середину.

В MatLab поиск локального минимума осуществляет функция fminbnd(), имеющая следующий формат:

[x, y] = fminbnd(name, a, b),где:

name– имя функции, вычисляющей значение f(x);

a, b – границы интервала, на котором осуществляется поиск минимума;

x, y – координаты точки минимума на заданном интервале.

Чтобы с использованием функции Matlab fminbnd() вычислить локальный максимум, необходимо взять целевую функцию с противоположным знаком.

Пример 2.5.1-1. Найти локальный минимум функции .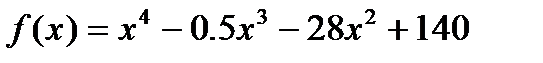

Решение задачи начнем с построения графика (рис. 2.5.1-1 и 2.5.1-2). Определим отрезок, содержащий точку минимума, исходя из вида графика функции. Если это возможно, то на этом отрезке следует провести полное исследование функции на унимодальность: от функции получить и первую, и вторую производные и показать, что 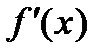должна быть неубывающей, а .

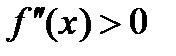Рис. 2.5.1-1. Построение графика функции f(x)

Рис. 2.5.9-2. График функции f(x)

Из графика следует, что на отрезках [-4;-3] и [3;5] имеются локальные минимумы. Исследуем функцию и поведение производных, например, на отрезке [3;5].

Для вычисления производных используем функцию Matlab diff(), имеющую следующий формат: diff(f, x, n). В качестве параметров этой функции используется:

· F– дифференцируемая функция;

· x– аргумент функции (переменная дифференцирования);

· n– порядок производной.

Получение значений функции и производных на выбранном отрезке приведено на рис. 2.5.1-3.

Рис. 2.5.1-3. Исследование функции f(x) на отрезке [3;5]

Из полученной таблицы значений функции и производных видно, что на отрезке [3;5] существует единственный минимум. Найдем координаты этого минимума с использованием функции Matlab fminbnd()(рис. 2.5.1-4).

Рис. 2.5.1-4. Нахождение координат точки минимума функции f(x)