Последовательный колебательный контур

Принципиальная схема контура (рис. 3.9, а) не позволяет оценить все электрические свойства цепи. Для анализа процессов, протекающих в контуре, необходимо перейти к схеме замещения путем замены каждого реального элемента его схемой замещения.

На рис. 3.9, б индуктивная катушка и конденсатор представлены простейшими последовательной и параллельной соответственно схемами замещения. Для контуров, применяемых в радиотехнике R_L имеет порядок единиц или десятков Ом, в то же время как R_C ≈ 10⁹ Ом и выше. Поэтому на практике влиянием R_C можно пренебречь и рассматривать схему на рис. 3.9, в, в которой R = R_L. Сопротивление R называют сопротивлением потерь. Оно характеризует преобразование электрической энергии контура в другой вид энергии.

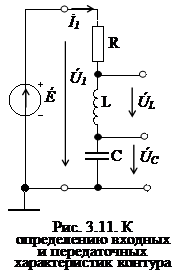
Рассмотрим колебательный контур, подключенный к источнику гармонических колебаний (рис. 3.10).

Контур как двухполюсник можно задать комплексными сопротивлением Z(jω) или проводимостью Y(jω)

. (3.14)

Резистивная часть сопротивления равна сопротивлению потерь контура r = R и не зависит от частоты.

Мнимая часть x(ω) = ωL – 1/ωC зависит от частоты и определяется разностью модулей сопротивлений индуктивности и емкости.

Комплексная амплитуда тока равна

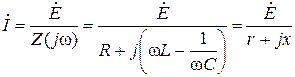(3.15)

Фазовый сдвиг между током и приложенным напряжением равен

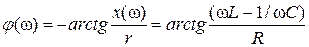. (3.16)

При определенном значении частоты источника ω = ω₀ реактивная часть комплексного сопротивления x(ω₀) будет равна нулю x(ω₀) =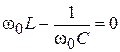

Решив это уравнение, получим значение частоты

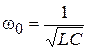. (3.17)

Это значение частоты называют резонансной частотой.

Полное сопротивление контура на резонансной частоте минимальное и равно сопротивлению потерь:

Z(ω₀) = R. (3.18)

Фазовый сдвиг между током и напряжением (3.16) на этой частоте в контура равен нулю φ(ω₀) = 0.

На резонансной частоте ток в контуре (3.15) будет максимальным

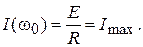(3.19)

Полное сопротивление индуктивности и емкости на резонансной частоте

равны: . (3.20)

Величину ρ, равную полным сопротивлениям реактивных сопротивлений L и C на резонансной частоте, называют характеристическим сопротивлением.На частотах до нескольких сотен мегагерц используют контура, у которых ρ = 0.1 – 1 кОм.

Амплитуды напряжений на реактивных элементах контура на резонансной частоте равны:

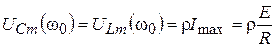. (3.21)

Резонансные свойства контура характеризуются параметром, называемым добротностьюQ:

. (3.22)

Добротность показывает, во сколько раз резонансное напряжение на реактивных элементах превышает приложенное напряжение на резонансной частоте. Поэтому в последовательном контуре резонанс называют резонансом напряжений. Как правило, добротность лежит в пределах от нескольких десятков до нескольких сотен.

Величина обратная добротности, называется затуханием контура d.

.

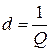а)

Величины ω₀, ρ, Q, d называются вторичными параметрами контура в отличие от величин R, L, C, называемые первичными.