Построение зубчатого зацепления
Зубчатую передачу строим следующим образом:
1. Откладываем межосевое расстояние 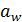 и проводим окружности: начальные
и проводим окружности: начальные  и
и 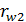 ; делительные
; делительные  и
и 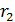 и основные
и основные  ,
,  ; окружности вершин
; окружности вершин  ,
, 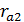 и впадин
и впадин  ,
,  . Начальные окружности касаются в полюсе зацепления. Расстояние между окружностями по осевой линии, равно воспринимаемому смещению ym. Расстояние между окружностями вершин одного колеса и впадин другого, измеренное по осевой линии, равно радиальному зазору
. Начальные окружности касаются в полюсе зацепления. Расстояние между окружностями по осевой линии, равно воспринимаемому смещению ym. Расстояние между окружностями вершин одного колеса и впадин другого, измеренное по осевой линии, равно радиальному зазору  .
.
2. Через полюс зацепления касательно к основным окружностям колес проводят линию зацепления. Точки касания 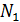 и
и 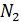 называют предельными точками линии зацепления. Линия зацепления образует с перпендикуляром, восстановленным к осевой в полюсе, угол давления. Буквами
называют предельными точками линии зацепления. Линия зацепления образует с перпендикуляром, восстановленным к осевой в полюсе, угол давления. Буквами  и
и  отмечена активная линия зацепления. Точка
отмечена активная линия зацепления. Точка  является точкой пересечения окружности вершин колеса с линией зацепления и называется точкой начала зацепления, а точка
является точкой пересечения окружности вершин колеса с линией зацепления и называется точкой начала зацепления, а точка  является точкой пересечения окружности вершин шестерни с линией зацепления и называется точкой конца зацепления.
является точкой пересечения окружности вершин шестерни с линией зацепления и называется точкой конца зацепления.
3. На каждом колесе cтроим профили зубьев, причем точка K должна располагаться на активной линии зацепления. Эвольвентную часть профиля зуба колеса строим как траекторию точки прямой при перекатывании ее по основной окружности колеса без проскальзывания. Переходную часть профиля зуба строим приближенно. От построенного профиля зуба откладываем толщину зуба по делительной окружности и проводим аналогичный профиль другой стороны зуба. Профили других зубьев располагаются на расстоянии шага 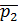 . На зубьях, касающихся в точке K, отмечаем активные профили, которые взаимодействуют в процессе зацепления. Нижние точки активных профилей лежат на пересечении окружностей
. На зубьях, касающихся в точке K, отмечаем активные профили, которые взаимодействуют в процессе зацепления. Нижние точки активных профилей лежат на пересечении окружностей  и
и  и соответствующих профилей. Активные профили перекатываются друг по другу со скольжением, поэтому длины их различны.
и соответствующих профилей. Активные профили перекатываются друг по другу со скольжением, поэтому длины их различны.
4. На чертеже проектируемой зубчатой передачи указываем диаметры начальных, делительных, основных окружностей, окружностей вершин и впадин, шаг и толщина зубьев по делительным окружностям, высота зубьев, межосевое расстояние, воспринимаемое смещение, угол зацепления, радиальный зазор, положение профилей в точках начала и конца зацепления, углы торцевого перекрытия  и
и 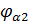 .
.
Проектирование планетарного редуктора.
Исходные данные для проектирования.
- число сателлитов 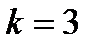 ;
;
- модуль  ;
;
- передаточное число редуктора:
 ; (здесь
; (здесь 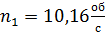 - число оборотов коленчатого вал;
- число оборотов коленчатого вал;  - число оборотов электродвигателя). Выбираем значение
- число оборотов электродвигателя). Выбираем значение 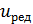 из ряда нормальных величин (
из ряда нормальных величин (  .
.
Подбор чисел зубьев.
1) Уравнение передаточного отношения:
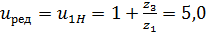 ;
;

2) Уравнение соосности (принимаем зубья колес планетарного редуктора без смещения):

3) Уравнение сборки:
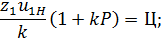
где P = 0, 1, 2, 3 … - целое число; Ц – любое целое число.
4) Условие соседства:
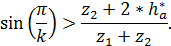
Критерии оптимальности:
1) Наибольший радиальный размер  или
или 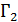 : Г
: Г  , если
, если 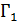 >
> 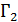 ;
; 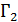 , если
, если 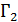 >
> 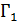 ;
;
2) Сумма чисел зубьев  , косвенно определяющая массу и трудоемкость изготовления;
, косвенно определяющая массу и трудоемкость изготовления;
3) Условие отсутствия кратности числу сателлитов k числа зубьев центральных колес.
Выбор числа зубьев колес.
Задаем число зубьев центрального колеса: 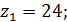
Из 1) Þ 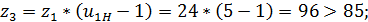
Из 2) Þ 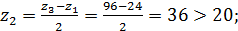
Проверяем условие сборки по 3) при Р = 0:
 - целое число, т.е. условие сборки выполняется.
- целое число, т.е. условие сборки выполняется.
Проверяем условие соседства по 4):

0,86>0,22 - условие соседства выполняется.
Выбранное количество зубьев колес редуктора:
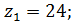


Определяем радиусы делительных окружностей колес: