Дифференциальные уравнения

Краткие теоретические сведения

Основные понятия о дифференциальных уравнениях

Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную х, искомую функцию
y = y(x) и ее производные 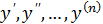. Символически ДУ можно записать в виде: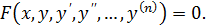

Если искомая функция есть функция одной независимой переменной, то ДУ называется обыкновенным.

Порядком ДУ называется порядок наивысшей производной, входящей в уравнение.

Примеры.

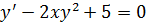
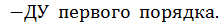
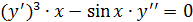
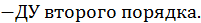
Решением ДУ называется всякая функция, которая при подстановке в уравнение обращает его в тождество. Общим решением ДУ называется такое его решение 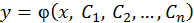, которое является функцией переменной х и n произвольных независимых постоянных С­₁, С₂, …, С_n (независимость постоянных – отсутствие каких-либо соотношений между ними). Частным решением ДУ называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных. Если общее решение записано в неявном виде 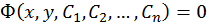, то его называют общим интегралом.

Задача о нахождении решения некоторого ДУ называется задачей интегрирования данного ДУ. График решения ДУ называется интегральной кривой. Графики всех решений представляют собой семейство интегральных кривых.

Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка имеет вид 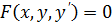, где х – независимая переменная, у – искомая функция, y’ – ее производная. Иногда в ДУ первого порядка встречается другая запись производной: .

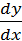Если ДУ первого порядка можно разрешить относительно производной, то его можно записать в виде: .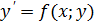

Теорема Коши (теорема существования и единственности решения ДУ). Если функция f (x; y) и ее частная производная по y определены и непрерывны в некоторой области D плоскости хОу, то какова бы ни была внутренняя точка (x₀; y₀) области D, в некоторой окрестности этой точки существует и при том единственное решение ДУ y’ = f(x; y), удовлетворяющее условиям y = y₀ при x = x₀.

Условия y = y₀ при x = x₀ называют начальными условиями или условиями Коши. Иногда их записывают в виде:

.

Задача Коши – это отыскание решения ДУ, удовлетворяющего начальным условиям. С геометрической точки зрения, решить задачу Коши, значит, из множества интегральных кривых выделить ту, которая проходит через заданную точку плоскости.

Точки плоскости, через которые проходит более одной интегральной кривой или не проходит ни одной интегральной кривой, называются особыми точками данного ДУ.