Динамические задачи управления запасами

В статических задачах управления запасами было рассмотрено функционирование системы (модели) за один период. В некоторых из них получены аналитические выражения для оптимального запаса (в частности, в детерминированной модели со стационарным спросом и периодическими поставками). Отметим, что эти задачи первые, для которых был создан и применен метод динамического программирования.

Если рассматривается функционирование системы за n периодов, причем спрос нестационарный, то имеем динамические модели задач управления запасами. Такие задачи, как правило, не допускают аналитического решения, однако оптимальную стратегию управления можно найти, применив метод динамического программирования.

1. Пусть рассматривается задача управления запасами на nпериодов, когда спрос за -й период детерминированный и определяется величиной , .

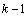Введем такие обозначения: - остаток запаса от ( )-го периода; - спрос в 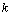-м периоде ( ); 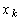- запас, создаваемый в 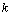-м периоде (или заказ на поставку).

Предположим, что заявка на поставку выполняется мгновенно, причем расходы на выполнение заказа (производственные затраты) обозначим через . Пусть - затраты по хранению избыточного запаса в 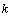-м периоде, причем дефицит в системе недопустим.

Тогда суммарные расходы системы по производству и хранению избыточных запасов за 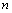периодов составляют

(7.4.1)

при ограничениях

, .

Требуется найти такие , для которых (7.4.1) обращается в минимум. Чтобы минимизировать , воспользуемся метдом динамического программирования. Последовательно будем минимизировать затраты на 1, 2, ., 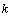периодов при условии, что на начало ( )-го периода есть избыточный запас 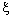. Определим последовательность функций состояния

(7.4.2)

при ограничении

. (7.4.3)

Тогда основное рекуррентное соотношение ДП запишется так:

(7.4.4)

где

На первом шаге (при ) получим:

при ограничении

Вычислив последовательно , , ., , на последнем шаге, приняв , найдем и . Оптимальные значения находим дальше последовательно по формуле

. (7.4.5)

2. Рассмотрим частный случай, значительно упрощающий вычислительную схему ДП. Предположим, что:

все функции вогнуты по переменным ;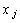

функции затрат на хранение запасов линейны, то есть

Тогда общее выражение для функции затрат будет иметь вид

(7.4.6)

при ограничении

, . (7.4.7)

Предположим, что заданы, заказы на поставки запасов выполняются в начале периодов, временем на выполнение заказа пренебрегаем (поставки мгновенные), а спрос каждого периода должен быть удовлетворен полностью (дефицит не допускается). Надо отыскать такие последовательности , минимизирующие функцию общих затрат (7.4.6).

Рассмотрим процедуру решения. Поскольку нужно найти минимум суммы вогнутых функций на выпуклом множестве, то оптимальным решением будет одна из крайних точек допустимого множества решений, определяемого ограничением (7.4.7).

Поскольку количество ограничений равно 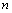, а общее число переменных и равно , то оптимальное решение содержит не более чем 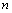ненулевых значений переменных. С учетом того, что не могут быть равны нулю одновременно (в противном случае не будет выполняться (7.4.7)), оптимальное решение обладает свойством:

. (7.4.8)

Условие (7.4.8) эквивалентно следующей паре условий:

(7.4.9)

Поясним смысл условий (7.4.8), (7.4.9). Заказ на изготовление (поставку) новой партии 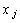не поступает, если в начале периода 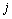имелся ненулевой запас ( ), и наоборот, если в начале периода 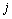запас , то делается заказ на поставку . Отсюда следует, что = 0, или = , или = и т.д., то есть оптимальный размер заказа равен спросу за целое число периодов.

Предположим, что . Тогда решаем задачу (7.4.6) в прямом направлении. Пусть - минимальные затраты за 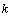периодов, если запас на начало ( )-го периода равен 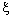. Основное рекурентне соотношение ДП для этой задачи имеет вид

(7.4.10)

при ограничении

, .

В рассматриваемом случае, поскольку , то минимум в (7.4.10) в силу вогнутости функции достигается в одной из крайних точек или .

Поэтому

(7.4.11)

Аналогично

(7.4.12)

Выписав выражения, аналогичные (7.4.12), для , , ., и подставив их в (7.4.12), (7.4.11), получим в результате

. (7.4.13)

Здесь

(7.4.14)

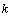где - затраты за периодов при условии, что последний заказ сделан в начале периода .

3. Рассмотрим частный случай функции производственных затрат на выполнение заказа . Пусть

(7.4.15)

где - фиксированные затраты на заказ;

(7.4.16)

Тогда

В этом случае задача упрощается и сводится к задаче ЛП:

минимизировать (7.4.17)

при ограничениях

. (7.4.18)

Используя выражения (7.4.15) - (7.4.17) и подставляя их в (7.4.14), получаем, с учетом , соотношение

(7.4.19)

. (7.4.20)

Дальнейшее упрощение в вычислительной схеме можно получить, если учесть следующее обстоятельство. Если при вычислении оказалось, что заказ, с помощью которого удовлетворялся спрос ( 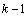)-го периода, должен поступить в начале периода , то и заказ, удовлетворяющий спрос 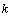-го периода в оптимальном решении, должен поступить также не ранее периода . Следовательно, при вычислении достаточно рассматривать

. (7.4.21)

Пример 7.3. Предприятие планирует поставку своей продукции на 7 месяцев в таких объемах: = 90 шт., = 125 шт., = 140, = 100, = 45, = 60, = 130. Затраты на хранение единицы продукции в течение месяца составляют = 2 грн.мес.; . Затраты на наладку оборудования (станков) для производства партии составляют = 300 грн.; . Причем наладка делается лишь в те месяцы, когда выпускается партия. Временем на выполнение заказа пренебрегаем. Требуется определить месяцы, когда производятся заказы, а также оптимальные размеры партий , .

Предположим, что в начале первого месяца не было никакого запаса, то есть .

Требуется

минимизировать ,

где =1, если и =0, если ,

при ограничениях

= 90,

, .

Используя соотношения (7.4.19), (7.4.21), имеем:

k = 1 ;

k = 2 ; .

Таким образом, только при двух периодах выгоднее выполнять лишь один заказ в первом периоде:

k = 3

; i = 3.

Результаты остальных вычислений приведены в табл. 7.10.

Таблица 7.10

Период k
Спрос d_k
	i = 1	550^*

g_k(i)			850^*	1050^*	1230^*

						1470^*

							1770^*
Λ_k(0)

V

В последней строке таблицы 7.10 указаны номера тех месяцев, в которые выполнялись заказы. Звездочки над указывают на то, что данное значение является минимальным по в соответствующем столбике (то есть равно ).

Покажем, как последовательно с табл. 7.10 определить периоды выполнения заказов при . Минимум в столбце достигается при ( = 1770).

Поэтому переходим к задаче при . Минимум в шестом столбце достигается при . Следовательно, последний заказ выполнялся в пятом месяце. Тогда переходим к и находим, что минимум при достигается при . Тогда переходим к и сразу находим, что минимум в столбце достигается при . Таким образом, номера месяцев, когда заказ выполняются, следующие: 1, 3, 5, 7.