Методика выполнения задания

Лабораторная работа № 12

Вычисление производной функции

Вычисление определенных интегралов

Цель работы: выработать навык использования табличного процессора MS Excel для численного (приближенного) вычисления производных функций (дифференцирование) и определенных интегралов (интегрирование), заданных в табличном виде.

Задание 1

Вычисление производной функции

Для функции своего варианта, используя MS Excel, вычислить производную в точках заданного интервала тремя способами: правых конечных разностей, левых конечных разностейицентральных разностей. Построить совмещенные графики вычисленных производных.

Методика выполнения задания.

Способы вычисления производной функции, заданной в табличном виде:

способ правой конечной разности

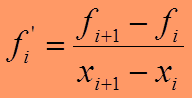
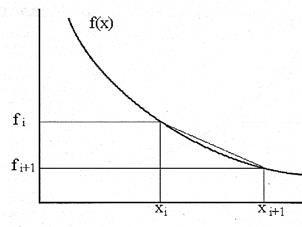
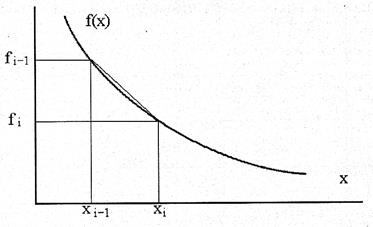
способ левой конечной разностью

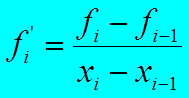
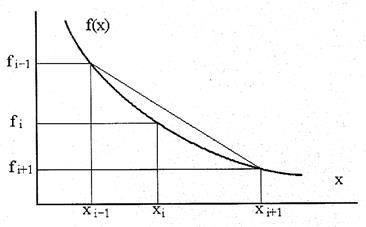
способ центральных разностей

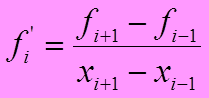
Вычисление производных на границе интервала, где задана функция, имеет свои особенности. Несложно догадаться, что, например, если вычислять производные согласно формуле для правых разностей, на правой границе диапа­зона производную вычислить не удастся. Для формулы левых разностей пробле­мы возникают, соответственно, на левой границе. Что касается центральных раз­ностей, то формула не может использоваться на обеих границах интервала.

Пример

Вычислить производную функции 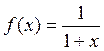на интервале [0; 5].

Аналитически производная выражается формулой .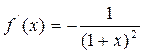

На рисунке представлена функция, табулированная с шагом 0,5 и формулы вычисления производной перечисленными выше способами. Там же приведены и точные значения производной в соответствующих точках.

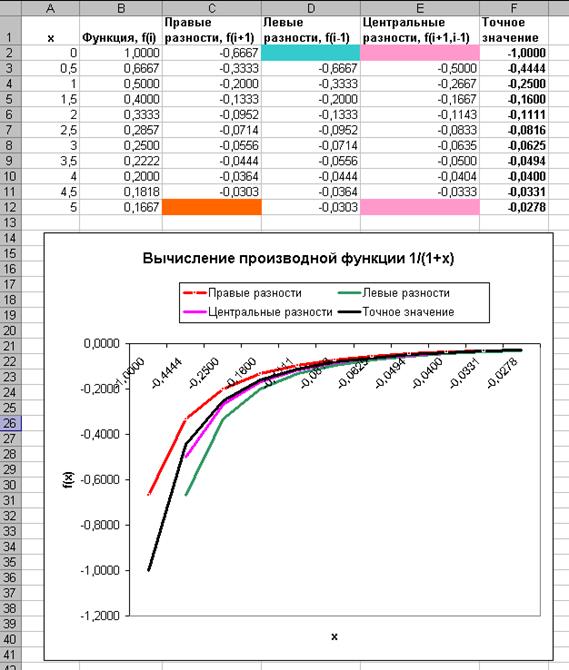интервала.

Порядок решения примера:

1. В ячейку А2 вводим 0 (начальное значение интервала) и с шагом 0,5 заполняем диапазон до значения 5 (конечная ячейка А12).

2. Вводим формулы:

В ячейку В2 =1/(1+A2) (функция 1/(1+x)) и копируем до ячейки В12;

В ячейку С2 (Правые разности) =(В3-В2)/(A3-A2)и копируем до ячейки С11;

В ячейку D3 (Левые разности) =(В3-В2)/(A3-A2)и копируем до ячейки D12;

В ячейку Е3 (Центральные разности) =(В4-В2)/(A4-A2)и копируем до ячейки E11;

В ячейку F2 (Точное значение) =−1/(1+A2)^2 (аналитически вычисленная производная -1/(1+x)^2) и копируем до ячейки F12.

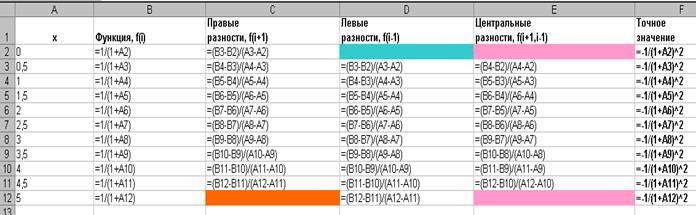
На рисунке приведено расположение формул в ячейках таблицы.

3. Строим совмещенные графики, вычисленной производной всеми способами и проводим анализ. При заданных начальных условиях ближе всего к точному решению находится результаты расчета способом центральных разностей.

Задание 1

В вариантных примерах Задания 1 шаг табулирования функции внутри интервала выбрать по формуле:

Шаг = (максимальное значение − минимальное значение) / 50.

Вариант	Функция	Интервал
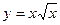		[10; 110]
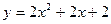		[1; 20]
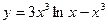		[0; 10]
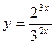		[0; 3]
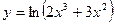		[4; 12]
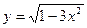		[0; 0,5]
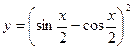		[0; p]
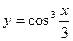		[0; p]
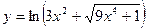		[1; 8]
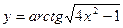		[2; 6]
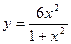		[1; 4]
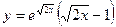		[0; 10]
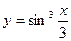		[0; 2]
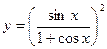		[1; 5]
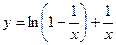		[10; 80]
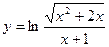		[1; 5]
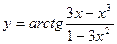		[0; 3]
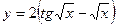		[0; 1]
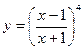		[2; 12]
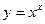		[1; 2]

Задание 2

Вычисление определенного интеграла

Методика выполнения задания.

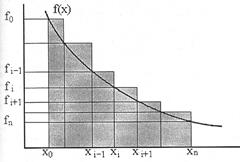
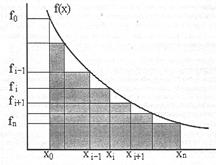
Наиболее простое и в большинстве случаев приемлемое приближение состоит в том, что на каждом из интервалов, на которые разбит диапазон интегрирования, ин­тегрируемая функция считается постоянной. В этом случае говорят о вычислении интеграла по формуле прямоугольников. При этом можно в качестве значения функ­ции на интервале брать либо значение на правой границе интервала (правосто­роннее приближение), либо значение на левой границе интервала (левостороннее приближение). Ситуация проиллюстрирована на рисунках.

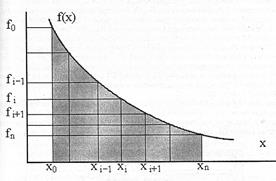Правостороннее приближение. Левостороннее приближение.

Приближение трапеций

Если все интервалы имеют одинаковую длину h, формулы имеют вид 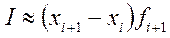для право­стороннего приближения и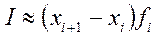 для левостороннего приближения. Однако обычно для вычисления интегралов используется формула трапеций. Она несколько слож­нее по сравнению с первыми двумя, но зато позволяет получать, как правило, более точные результаты. Идея состоит в том, что соседние узловые точки функции соеди­няются прямой, поэтому вся площадь под графиком функции состоит как бы из трапе­ций. Соответственно, сама площадь равна сумме площадей этих трапеций. Формула для интервалов равной длины имеет вид .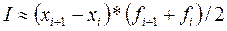

Это три основные формулы, позволяющие вычислять интегралы от функций, за­данных в виде таблицы.

Далее рассмотрим, как описанные методы могут использоваться для вычисления интегралов на практике.

Пример.

Вычислить интеграл .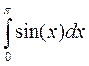

Этот интеграл может быть вычислен аналитически. В частности, очевидно, что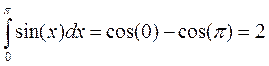

Именно это значение и попытаемся получить в результате интегрирования с использованием численных методов.

1. Оформляем таблицу, как показано на рисунке.

2. В ячейку А4вводим число 0 как начальное значение для переменной интегрирования. После этого в ячейку А5 вводится формула =А4+ПИ()/10, согласно которой значе­ние последующего узла получается прибавлением к предыдущему узлу десятой части от длины диапазона интегрирования (команда ПИ()/10) и копируем ее до А14.

3. В ячейку В4вводим заданную формулу =SIN(A4)и копируем ее до ячейки В14.

4. Вводим формулы для вычис­ления площадей элементарных (базовых) прямоугольников или трапеций.

В ячейку С4 вводим формулу =(А5 -А4)*В5 (правосторонние приближение), в ячейку D4вводим практически такую же формулу =(А5-А4)*В4 (левосторонние приближение), и для метода трапеций в ячейку Е4 вводится формула =(А5-А4)*(В5+В4)/2.

Заполнять данные для элементарных площадей следует вплоть до предпоследней строки диапазона (т.е. ячейки С14, D14, Е14 заполнять не следует — для этих ячеек введенные ранее формулы опреде­ления элементарных площадей не работают).

Осталось только вычислить сумму значений в столбцах С, D и Е. Для этого выде­ляем ячейку С15 и вводим туда формулу =СУММ(C4:C13).

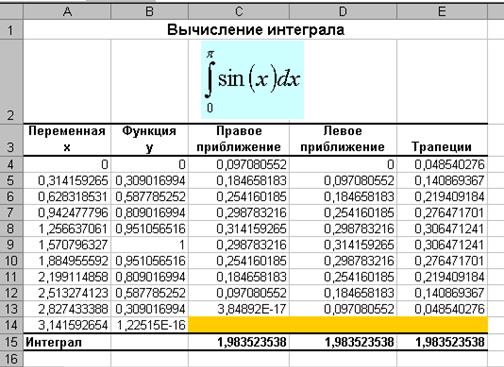В ячейку D15вводится формула =СУММ(D4:D13),а в ячейку Е15— формула =СУММ(E4:E13).Окончательный результат показан на рисунке.

Результат вычислений для всех методов получился одинаковый.

Абсолютная точность: |2−1,9835| = 0,0165.

Относительная точность: 0,0165 / 1,9835 = 0,0083.

В приведенном примере определенный интеграл может быть вычислен аналитически. Однако на практике часто возникают задачи, сводящиеся к вычислению интегралов данных представленных таблицей. Например, результаты эксперимента или записи наблюдений за изменением, какого либо параметра. С помощью метода аппроксимации преобразуют таблицу в формулу, которую впоследствии табулируют с равномерным шагом. Тогда вычисление заданной точности (погрешности) вычисляется по следующей формуле: 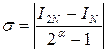, где N – количество точек (узлов) в начальной таблице, I − интеграл, a = 2 − для метода прямоугольников и метода трапеций.