Разностное уравнение и его характеристическое уравнение

На множестве значений дискретизированной по аргументу функции можно ввести известные операции сложения (вычитания), умножения (деления) и, в дополнение к ним, оператор смещения:

,

который по смыслу определяет выборку значения функции сдвинутой относительно исходного значения на «к» единиц влево (со знаком минус) или вправо.

Построим выражение, представляющее аналог первой производной (правой) для непрерывной по аргументу функции:

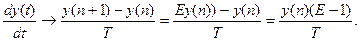
Получим выражение для второй производной:

Обозначим разность в скобках между оператором сдвига и единицей через Δ и назовём РАЗНОСТНЫМ оператором.

В этих обозначениях дискретные аналоги производных можем записать:

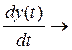y(n)Δ/Т,

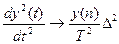
Полученные выражения для «производных» позволяют поставить вопрос о возможности написания уравнений в разностных представлениях, которые, в определённом смысле, подобны дифференциальным.

Как возникает разностное уравнение?

А как возникает дифференциальное уравнение?

Рассмотрим пример. Пусть имеется простейшая цепь, состоящая из тёх элементов, которые последовательны : источника напряжения, резистора и емкостного элемента.

По второму закону напишем

Последняя формула определяет величину тока в рассматриваемой цепи поскольку z непрерывная величина по комплексной частоте, то можно говорить о частотной характеристике в области дискретных частот.

Подобный подход позволяет начинать излагать теорию цепей с дискретных цепей.

Запись требует определение 2-х-полюсников в дискретной области через конечные приращения.

Начнём с экспериментальных данных по схемам.

Все кривые тока и напряжения представляем дискретным набором и пытаемся полученным графикам поставить в соответствие математическую операцию (оператор), связывающую функции тока и напряжения, которые заданы на одном и том же множестве значений времени.

Скачкообразное изменение в бесконечной малой области можно представить оператором смещения

Разовьём соображения относительно получения формулы, которая связывает параметры элементов в ПК-эквивалентах.

Вывод формул проведём для трёх ПК-эквивалентов.

Условием эквивалентности будем считать равенство зарядов, которые протекают через резистор и емкостной элемент за некоторый интервал времени Т в схеме с двумя источниками. Функции источников представляют дискретные по времени, которые можно представить как некоторые функции тока на интервале Т.

Рассмотрим ПРОЦЕСС получения дискретизированного напряжения во временной области и рассмотрим влияние процесса на характер его спектра (область мнимых частот).

Процесс получения во временной области можно представить произведением 2-х функций времени (см. схему с ключом)

u_1,1'(t)^* = u_1,1'(t) р(t),

в которой р(t) можно представить как последовательность прямоугольных импульсов, длительность которых много меньше периода следования Т. В пределе эту последовательность можно представить последовательностью δ(t) – импульсов.

Если K(t) периодическая последовательность, то её можно записать рядом Фурье

.

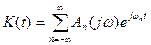Подставляя эту запись в предыдущую формулу, ПОЛУЧИМ

.

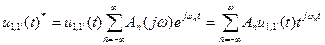Применим к обеим частям равенства интеграл Фурье и получим спектральную функцию дискретизированного напряжения:

.

Спектральная функция входного напряжения в рассматриваемом случае есть периодическая функция с периодом равным частоте первой гармоники для периодической последовательности K(t), т.е. 1/Т либо 2π/Т.

1.0. Инвариантность понятий «операторный ток» и «заряд»

В процессе вывода выражения для тока в схемах на переключаемых конденсаторах формируется выражение, в котором переменная в виде комплексной частоты сокращается и получается действительное выражение в правой части формулы. Следовательно, и левая часть также должна представлять действительное понятие, суть которого можно определить по размерности. Размерность А с,- что есть размерность электрического заряда.

Выведем операторное уравнение заряда для тока, протекающего в цепи с R, предназначенной для определения ПК - эквивалентов.

Итак, запишем формулу для тока и заряда:

.

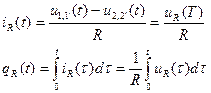Переведём формулу заряда в операторную область:

Запишем выражение для тока в этой цепи, при условии, напряжения источников есть дискретные по времени и имеющие постоянные значения, на некотором интервале Т.

Тогда, для схемы в операторной области, ток можно записать

.

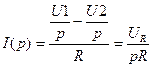Полученное выражение является аналогом выражения для операторного выражения для заряда.