Проверка результатов расчета
Проверка расчетов может быть выполнена в двух вариантах. Первый вариант – проверяется только этап аппроксимации, когда определяется насколько точно созданная передаточная функция соответствует исходным требованиям к фильтру по ослаблению в ПП и в ПН. Второй вариант – проверяется точность уже всего расчета, когда по известной передаточной функции схемы фильтра (т. е. с учетом значений элементов схемы) рассчитывается и строится график H(f) или А(f) всей схемы фильтра и анализируется, насколько хорошо этот график соответствует исходных требованиям по ослаблению в ПП и в ПН. Конечно, второй вариант для разработчика предпочтительнее.
При синтезе пассивного полосового фильтра получена передаточная функция только НЧ-прототипа и в этом случае возможен только первый вариант проверки. При синтезе активного ПФ известна передаточная функция одного звена уже самой схемы фильтра. Очевидно, что Н(р) всего фильтра будет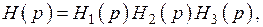 
где значения каждого сомножителя будут отличаться из-за разницы в значениях сопротивлений звеньев фильтра. Итак, эта формула позволяет реализовать второй вариант проверки выполненных расчетов.
С этой целью производится замена переменной вида р = jw, в результате чего получают выражение
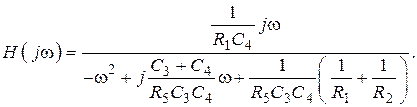
Находится модуль H(jw) в виде
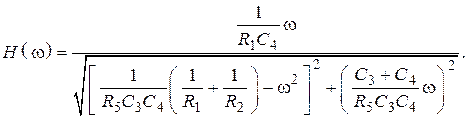
Зная H(w), легко найти зависимость ослабления от частоты вначале каждого звена, а затем всего фильтра:
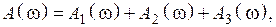где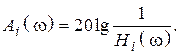 
Расчет ослабления на границах частот пропускания и непропускания:
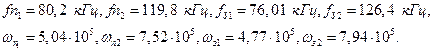
Все результаты сводятся в таблицу 3
При анализе табличных данных обращаем внимание на разный характер зависимости ослабления от частоты у разных звеньев фильтра.
| f, кГц | fз1 | fп1 | fп2 | fз2 |
| 76,01 | 80,2 | 119,8 | 126,4 | |
| Н1(w) Н2(w) Н3(w) | 0,478 1,881 0,234 | 0,601 4,242 0,27 | 0,61 0,391 3,109 | 0,485 0,34 1,373 |
| Н (w) | 0,21 | 0,69 | 0,74 | 0,23 |
| А1(w), дБ А2(w), дБ А3(w), дБ | -6,41 5,49 -12,61 | -4,42 12,55 -11,37 | -4,29 -8,16 9,85 | -6,29 -9,37 2,75 |
| А (w), дБ | -13,53 | -3,24 | -2,6 | -12,91 |
В ходе расчета мы обратили внимание на то, что значение Н(w) наиболее сильно зависит от величины сопротивления R2, поэтому именно это сопротивление необходимо выбирать переменным.
На рис. 8 приведена ожидаемая теоретическая кривая зависимости ослабления фильтра от частоты. На рис. 9 приведена принципиальная схема активного полосового фильтра.
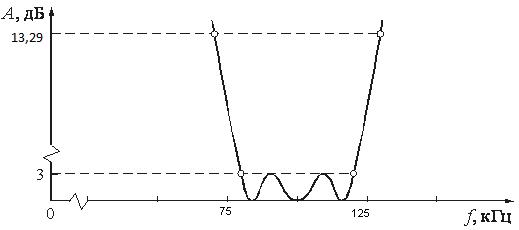
Рис. 8
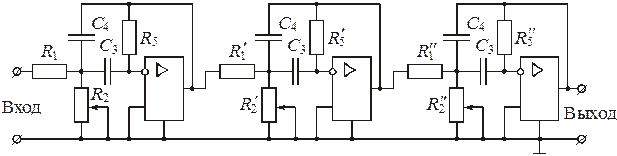
R1, R2, R5 – сопротивления 1-го звена
R¢1, R¢2, R¢5 – сопротивления 2-го звена
R²1, R²2, R²5 – сопротивления 3-го звена
Рис. 9
Литература
1. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей. Учебник – М.: Радио и связь, 2000. – 589 с.
2. Бакалов В.П., Воробиенко П.П., Крук Б.И. Теория электрических цепей. Учебник – М.: Радио и связь, 1998. – 444 с.
3. Белецкий А.Ф. Теория линейных электрических цепей. Учебник. – М.: Радио и связь, 1986. – 544 с.