Пример 2

Идеальный газ имеет полную энергию Е и состоит из N независимых молекул. Молекула имеет массу m и является одномерным гармоническим осциллятором, колеблющимся с частотой ω. Поступательные и вращательные движения молекул не учитывать. Найти энергетическую плотность состояний и температуру газа.

Гамильтониан газа складывается из энергий N осцилляторов

.

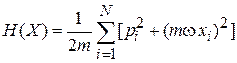Для изолированного газа 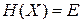и получаем уравнение эллипсоида в 2N-мерном пространстве

.

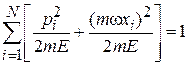Состояния газа с энергией E находятся в фазовом пространстве на поверхности эллипсоида с параметрами:

N полуосей ,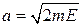

N полуосей ,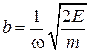

.

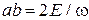Объем эллипсоида находим из (П.2.1а)

, ,

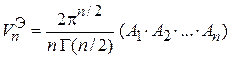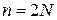получаем

.

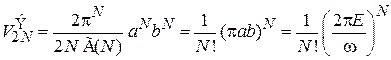Число микросостояний

,

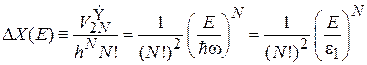где 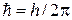; 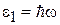– квант энергии осциллятора.

Энергетическая плотность состояний

,

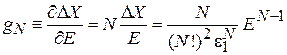тогда

.

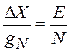Из (2.14)

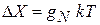
находим

, .

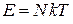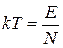Средняя энергия одномерного гармонического осциллятора

.
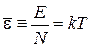