Дифференцирование функций

Дифференцирование можно выполнить численное, а можно символьное. Для получения численного значения производной, нужно выбрать кнопку производной из панели Исчисления, проставить переменную дифференцирования, ввести функцию в соответствующий место-заполнитель и поставить знак равенства <=>.

Для символьного дифференцирования нужно выполнить те же действия, что и при численном дифференцировании, только вместо знака равенства надо поставить знак стрелки <®> из панели Оценка. Например:

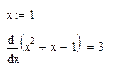
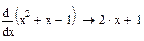
Вторая производная, третья и т. д.:

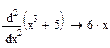
Задания.

Вычислить производную функции в числовом и символьном виде:

Номер варианта	f(x)	Номер варианта	f(x)
1.		12.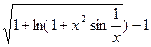
2.		13.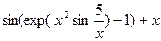
3.		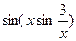14.
4.		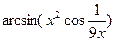15.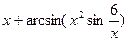
5.		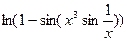16.
6.		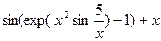17.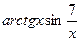
7.		18.
8.		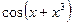19.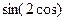
9.		20.
10.		21.
11.		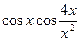22.

Вычисление определенных интегралов.

Для вычисления определенного интеграла нужно выбрать кнопку со знаком определенного интеграла из панели Исчисления, расставить пределы интегрирования, ввести функцию в соответствующий место-заполнитель, переменную интегрирования и знак равенства. Например:

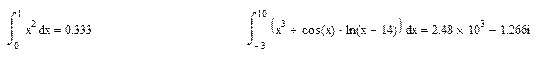
Задания.

Вычислить определенный интеграл:

Номер варианта	f(x)	[a,b]	Номер варианта	f(x)	[a,b]
1.		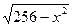[0,16]	12.		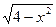[0,2]
2.		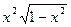[0,1]	13.		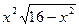[0,4]
3.		[0,5]	14.		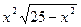[0,5]
4.		[3,5]	15.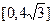
5.		[0, ]	16.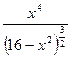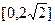
6.		[0, 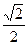]	17.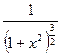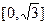
7.		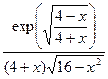[0,4]	18.		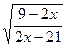[6,9]
8.	)	[0,1]	19.		[4,5]
9.		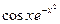[1,2]	20.		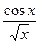[1,3]
10.		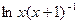[2,3]	21.		[4,5]
11.		[0, ]	22.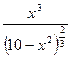

Вычисление неопределенных интегралов.

Для вычисления неопределенного интеграла нужно выбрать кнопку с его знаком с панели Исчисления, ввести функцию в соответствующий место-заполнитель, переменную интегрирования и знак стрелки <®> с панели Оценка.

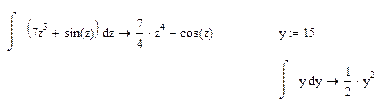
Задания.

Вычислить неопределенный интеграл:

Номер варианта	f(x)	Номер варианта	f(x)
1.		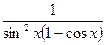12.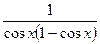
2.		13.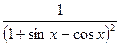
3.		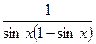14.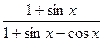
4.		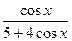15.
5.		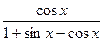16.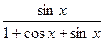
6.		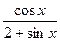17.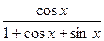
7.		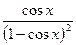18.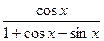
8.		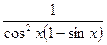19.
9.		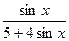20.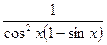
10.		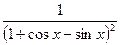21.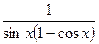
11.		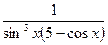22.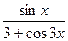

3.8 Вычисление сумм и произведений.

Для вычисления сумм и произведений используется панель Исчисления. Например:

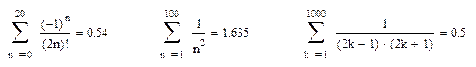
В приведенных примерах используется значок суммы с указанием границ суммирования. Из примеров видно, что в данном случае система обрабатывает ситуации: (-1)⁰=1 и 0!=1 (n!=1*2*…*n).

Знак суммирования с указанием только индекса используется в тех случаях, когда пределы изменения индекса заданы переменной интервального типа. Например:

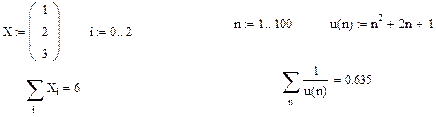
Аналогично вычисляются произведения. Например:

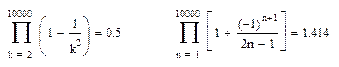
Например, выполним для матриц М и С следующие действия:

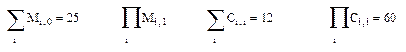
Задания.

Вычислить ошибку представления числового ряда в виде суммы при к=10 с точностью до шестого знака:

Номер варианта	f(x)	Номер варианта	f(x)
1.		12.
2.		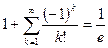13.
3.		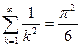14.
4.		15.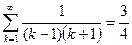
5.		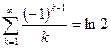16.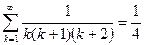
6.		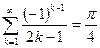17.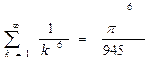
7.		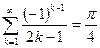18.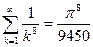
8.		19.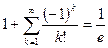
9.		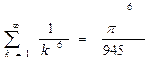20.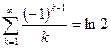
10.		21.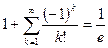
11.		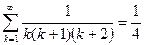22.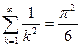

Структура курсовой работы

Текстовая часть курсовой работы оформляется в виде пояснительной записки в соответствии с требованиями стандарта [10, 11].

Результаты выполнения работы представляются в пояснительной записке в распечатанном виде. Результаты заданий курсовой работы должны быть приведены в электронном виде на любом носителе.

Содержание курсовой работы.