Выполним отделение корней графическим методом.

1 способ.

Корни отделяются просто, если построен график функции 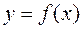. Точки пересечения графика с осью 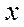дают значение корня, и по графику легко определить интервал 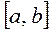, в котором находится только один корень.

-

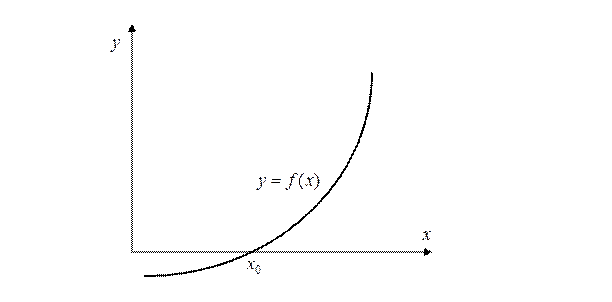
2 способ.

Уравнение имеет вид 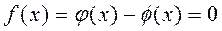. Все члены уравнения разбивают на две группы, одну из них записывают в левой части уравнения, другую – в правой, т.е. записывают уравнение в виде

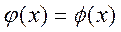
После этого строят графики функций и . Абсциссы точек пересечения графиков этих двух функций и являются корнями данного уравнения. По графику и определяют интервал , в котором заключен корень.

Уточнение корней методом проб (метод половинного деления)

Итак, выполнен первый этап – отделение корня.

Второй этап заключается в уточнении корней, в вычислении корней с заданной точностью.

Пусть дано уравнени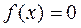е , где - непрерывная функция. Требуется найти корень этого уравнения 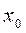с точностью до величин 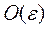, где 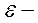малое, нами заданное число.

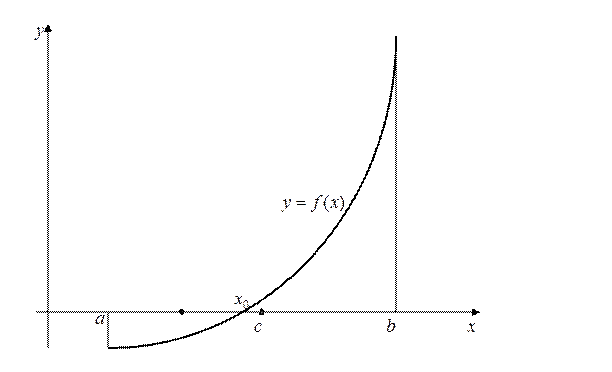
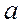Будем считать, что выполнено отделение корня и известно, что корень находится в интервале . Числа и 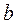можно рассматривать как приближенные значения корня, 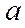- значение корня с недостатком, а 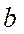- с избытком. Погрешность этих вычислений не превышает величины . Если 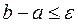, то необходимая точность вычислений достигнута, и за приближенное значение корня 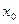можно принять либо , либо 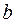. Если же , то требуемая точность не достигнута и необходимо сузить интервал, в котором находится корень 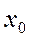. Для этого на отрезке 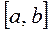выберем точку 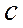, которая делит отрезок пополам 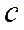=(a+b)/2 (в этом случае метод проб называют методом половинного интервала). Если 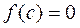, то 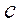- точный корень уравнения 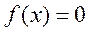. Если же 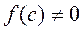, то из двух полученных отрезков и 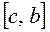выберем тот, на концах которого функция принимает значения противоположных знаков. Затем этот отрезок также делим пополам и проводим те же рассуждения. Процесс деления отрезка пополам продолжаем до тех пор, пока на каком – то этапе либо середина отрезка окажется корнем уравнения (случай, теоретически возможный, но чрезвычайно редко встречающийся на практике), либо отрезок, длина которого меньше заданной малой величины .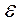

Задание.

Задан полином третьей степени

,

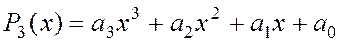где

Требуется вычислить корень полинома на отрезке

(требуется составить программу в системе MATLAB (M-языке) методом половинного деления или методом Ньютона (по указанию преподавателя)).

В критериях окончания счета на ЭВМ для обоих методов принять

eps=0.001, xk=3 .

Пример

Найти корни полинома 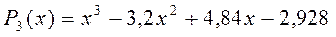на отрезке ,

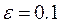
Ручной счет

Вычисление корня методом половинного деления

K	а	b	c=(a+b)/2	f(a)	f (b)	f(c)	b-a
		3.0	1.5	-2.92	9.79	0.51	3.0
		1.5	0.75	-2.92	0.51	-0.67	1.5
	0.75	1.5	1.125	-0.67	0.51	-0.11	0.75
	1.125	1.5	1.3125	-0.11	0.51	0.173	0.375
	1.125	1.3125	1.218	-0.11	0.173	0.0267	0.187

Решение нелинейного уравнения методом половинного деления.

Для выполнения создается М-файл. Ниже приведен текст М-файла.

%Решение нелинейного уравнения методом половинного деления

function Lab_3_6_1

a=input('Введите a=');

b=input('Введите b=');

eps=input('Введите eps=');

kmax=100;

for k=1:kmax

c=(a+b)/2;

y=f(c);

if(f(a)*y>0)

a=c;

else

b=c;

end

if((b-a)<=eps)|(y==0)|(k>=kmax)

x=c;

break;

end

end

fprintf('\n Корень уравнения x=%10.3f ',x);

fprintf('\n f(x)=%12.4g',y);

fprintf('\n Количество итерации k=%3d',k);

end

function y=f(x)

y=x^3-3.2*x^2+4.84*x-2.928;

end

Результаты расчета в командном окне при a=0, b=0, eps=0.001:

Корень уравнения x= 1.200

f(x)= 0.0006505

Количество итерации k= 12

Решение нелинейного уравнения методом Ньютона.

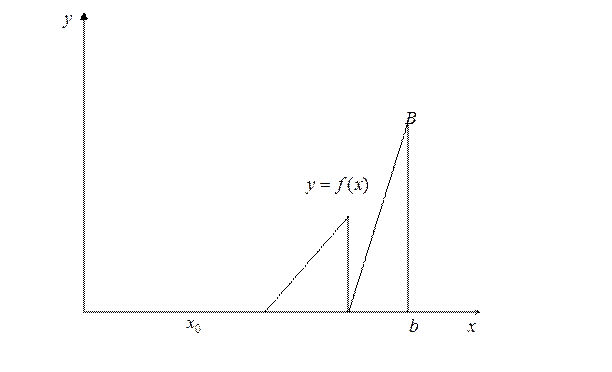
Пусть корень уравнения 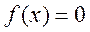отделен на отрезке 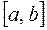. Причем

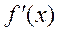, непрерывны и сохраняют постоянные знаки на всем отрезке .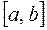

Геометрический смысл метода Ньютона состоит в том, что дуга кривой 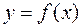заменяется касательной к этой кривой.

Пусть , , 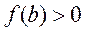, 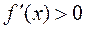. В этом случае касательную проводим в точке B.

Уравнение касательной в точке B имеет вид

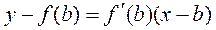
при , получим

Теперь корень уравнения находится на отрезке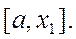

Продолжая процесс, найдем

Ручной счет

k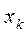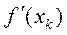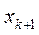
	3.0	9.79	12.64	2.22	0.78
	2.22	3.01	5.45	1.67	0.55
	1.67	0.89	2.52	1.32	0.35
	1.32	0.18	1.62	1.20	0.12
	1.2				Критерий окончания счета

Напишем программу вычисления отделенного корня с точностью до величин порядка 0,001.

Для выполнения создается М-файл. Ниже приведен текст М-файла.

Решение нелинейного уравнения методом Ньютона.

function Lab_3_6_2

xk=input('Введите xk=');

eps=input('Введите eps=');

kmax=100;

for k=1:kmax

y=f(xk);

y1=f1(xk);

xk1=xk-y/y1;

if(abs(xk1-xk)<eps)|(k>kmax)

break;

end

xk=xk1;

end

y2=f(xk1);

fprintf('\n Корень уравнения x=%10.3f',xk1);

fprintf('\n f(x)=%12.4g',y);

fprintf('\n Количество итерации k=%3d',k);

end

function y=f(x)

y=x^3-3.2*x^2+4.84*x-2.928;

end

function y1=f1(x)

y1=3*x^2-6.4*x+4.84;

end

Результаты расчета в командном окне при xk=3, eps=0.001:

Корень уравнения x= 1.200

f(x)= 0.0009755

Количество итерации k= 3

В системе MATLAB имеется большое количество функций для работы с полиномами, с использованием которых можно вычислить значение полинома, найти корни полинома, выполнить операции умножения и деления полиномов, произвести дифференцирование и интегрирование полиномов.

Как известно, полином (или многочлен) — это выражение вида

P_n(x)=a_nxⁿ+a_n-1x^n-1+...+a₂x²+a₁x+a₀

где a₀, a₁, a₂, …, a_n-1, a_n — постоянные коэффициенты.

В MATLAB полином задаётся и хранится в виде вектора, элементами которого являются коэффициенты полинома

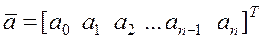
Так, например, для задания полинома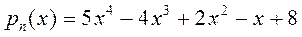

следует ввести команду

>> p=[5 -4 2 -1 8]

p =

5 -4 2 -1 8