Неопределенный и определенный интегралы.

Раздел 3.

ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

1. Условия возрастания и убывания функций.

2. Точки экстремума. Необходимые условия экстремума.

3. Отыскание наибольшего и наименьшего значения функции на отрезке.

4. Исследование функций на выпуклость и вогнутость. Точки перегиба.

5. Асимптоты кривых.

6. Общая схема построения графиков функций.
Литература , гл. V, §2-6; §9-12, упр. 1,2,8,11,14,19, 32-34,62,63,72,75,76,83,84.

7. Функции нескольких переменных. Основные понятия (область определения, предел функции, непрерывность)

8. Частные производные, Полный дифференциал. Вычисление приближенного значения функции с помощью дифференциала. Касательная плоскость и нормаль к поверхности.

9. Экстремумы функции нескольких переменных.
Литература , гл. VIII, §1,2,3,5,6,7,8,10,11,12,16,17,19.

10. Уравнение кривой в пространстве.

11. Уравнение касательной к кривой. Уравнение нормальной плоскости.

12. Кривизна кривой.

Литература , гл. IX, §1-4, упр. 1,2,4,5,13

Вопросы для самопроверки.

1. Дайте определение возрастающей (убывающей) функции на промежутке.

2. Что называют интервалами монотонности функции?

3. Какие углы образуют касательные к графику возрастающей (убывающей) функции с положительным направлением оси абсцисс?

4. Приведите примеры возрастающих и убывающих функций и укажите их интервалы возрастания и убывания.

5. Сформулируйте правило нахождения интервалов монотонности функции.

6. Покажите, что функции и возрастают в любом промежутке.

7. Дайте определение максимума (минимума) функции.

8. Какие точки называют точками экстремума функции?

9. Сформулируйте необходимое условие экстремума функции. Является ли оно достаточным условием?

10. Какие точки называются критическими точками функции?

11. Сформулируйте правило (последовательность ваших действий) нахождения экстремума функции.

12. Дайте определение наибольшего (наименьшего) значения функции на отрезке.

13. Всегда ли существуют у функции на отрезке наибольшее и наименьшее значения?

14. Сформулируйте правило нахождения наибольшего и наименьшего значения функции, дифференцируемой на отрезке.

15. Если функция непрерывна на промежутке, который не является отрезком, обязана ли она иметь на этом промежутке наибольшее и наименьшее значение?

16. Какую кривую называют выпуклой (вогнутой) на интервале?

17. Сформулируйте достаточный признак выпуклости (вогнутости) кривой на интервале.

18. Какую точку называют точкой перегиба? Что происходит со второй производной в точке перегиба?

19. Сформулируйте достаточный признак точки перегиба.

20. Сформулируйте определение асимптоты кривой.

21. В точках разрыва какого рода ищут вертикальные асимптоты?

22. Как находятся наклонные и горизонтальные асимптоты?

23. Изложите схему общего исследования функции и построения ее графика.

24. Когда функция называется дифференцируемой в данной точке . Что называется полным дифференциалом этой функции в данной точке? В чем состоит правило применения полного дифференциала для вычисления приближенного значения функции, близкого к известному?

25. Выведите уравнения касательной плоскости и нормали к поверхности в точке М. Выясните геометрический смысл полного дифференциала функции двух переменных.

26. Дайте определение частных производных высших порядков. Сформулируйте теорему о равенстве смешанных частных производных функции двух переменных.

27. Что называется производной функции в данной точке М_о по направлению вектора ? Выведите формулу ее вычисления.

28. Что называется градиентом скалярного поля в данной точке? Как выражается производная по направлению через градиент и единичный вектор?

29. Дайте определение локального максимума (минимума) функции двух переменных. Выведите необходимое условие и сформулируйте достаточное условие экстремума функции двух переменных.

30. Сформулируйте правило нахождения экстремумов функции двух переменных.

31. Выведите правило нахождения наибольшего и наименьшего значения функции двух переменных в замкнутой области.

32. Что называется условным экстремумом функции ? Как найти условный экстремум функции двух переменных, если эти переменные связаны одним условием?

33. Напишите уравнения касательной и нормальной плоскости к кривой.

34. Как вычислить кривизну кривой в данной точке?

Пример 1. Провести полное исследование и построить график функции

1) Найдем область определения. Функция f(x) является частным случаем «склеенной» функции, т.е. функции вида

.

Иногда множества D₁ и D₂ полностью не указываются. Надо учитывать естественные области определения функций f₁(x) и f₂(x). В нашем примере f₁(x)=1, D₁= , f₂(x)= и D₂ : .

Итак, область определения функции f(x): . Причем значение х=0 - точка «склеивания».

В дальнейшем каждую из функций f₁(x) и f₂(x) исследуем соответственно в областях D₁ и D₂, и поведение каждой из функций в окрестности точки «склеивания».

Так как f₁(x)=1 - const, график функции на области D₁ можно построить без дополнительных исследований.

Исследование функции f₂(x).

а) Корни f₂(x)=0

х =1, х = -1;

б) Промежутки знакопостоянства f₂(x):

в) Поведение f₂(x) в граничных точках области определения:

Прямая является вертикальной асимптотой.

Наклонная асимптота:

Прямая является наклонной асимптотой на .

г) Для отыскания интервалов возрастания и убывания функции найдем первую производную

Критических точек нет, так как . Интервалы знакопостоянства :

+ +

0

возрастает на промежутках и .

д) Для отыскания областей выпуклости и вогнутости найдем вторую производную

Критических точек нет. Интервалы знакопостоянства :

+ -

0

График функции вогнут на промежутке .

График является выпуклым на промежутке .

е) Исследуем теперь функцию f(x) в окрестности точки «склеивания» х = 0

Функция f(x) непрерывна в точке х = 0.

Построим график функции:

Пример 2. Найти наибольшее и наименьшее значение функции

в замкнутой области, заданной системой неравенств

При отыскании наибольшего и наименьшего значения функции нескольких переменных в замкнутой области следует помнить, что точки, в которых достигается наибольшее и наименьшее значение, могут находиться: 1) внутри области; 2) на границах области; 3) в точках пересечения границ области.

1. Найдем точки, подозреваемые на экстремум.

Решив систему, получим две точки . Точка принадлежит области. Точка - лежит на границе (точка А). Обе точки принадлежат области. Значение функции в этих точках.

2. Исследуем границы области.

а) (АВ) имеет уравнение х = 0. На этой границе функция примет вид (зависит от одной переменной). Найдем точки, подозреваемые на экстремум, это точки, в которых или не существует при . Получили точку . Значение - уже вычислили.
б) Участок (ВС) имеет уравнение у = 0.

z зависит от одной переменной х, ее наибольшее и наименьшее значения находятся среди значений в критических точках.

при

не принадлежит участку (ВС). Найдем значение функции только в тех точках границы, которые принадлежат участку (ВС)

в) Участок границы (АС) имеет уравнение . На этом участке

.
Решая уравнение , т.е. , находим критические точки . Точки принадлежат участку границы (АС).
.

3. Находим значение функции в точках пересечения границ:

4. Наибольшее и наименьшее значение достигается в одной из найденных в процессе решения точек: . Сравнивая значения во всех этих точках, замечаем, что самое большое из них рано 12, а самое малое -1.
Ответ: .

Контрольные задания

Задание №1. Найти наибольшее и наименьшее значения функции f(x) на отрезке [a; b].

1.1. f(x)=x4-x2+5; [-2; 2]	1.2. f(x)=x+2 ; [0; 4]
1.3. f(x)=x5-5x4+5x3; [-1; 2]	1.4. f(x)=x3-3x2+6x; [-1; 1]
1.5. f(x)=x4-8x2+3; [-2; 2]	1.6. f(x)=(x3/3)-2x2+2; [-1; 2]
1.7. f(x)=x3-1,5x2-6x+1; [-2; 0]	1.8. f(x)=x4-8x2-8; [-1; 3]
1.9. f(x)=x3-6x2+9x; [-1; 4]	1.10. f(x)=3x-x3; [-2; 3]
1.11. f(x)=x3-12x+7; [0; 3]	1.12. f(x)=x5-(5/3)x3+2; [0; 2]
1.13. f(x)= x+cosx; [0; p/2]	1.14. f(x)=3x4-16x3+2; [-3; 1]
1.15. f(x)=x3-3x+1; [1/2; 2]	1.16. f(x)=x4+4x; [-2; 2]
1.17. f(x)= x-sinx; [0; p/2]	1.18. f(x)=81x-x4; [-1; 4]
1.19. f(x)=3-2x2; [-1; 3]	1.20. f(x)=x-sinx; [-p; p]
1.21. f(x)=x-4 ; [0; 9]	1.22. f(x)=x5+x4-3x3; [-1; 2]
1.23. f(x)=x-2sinx; [0; p/2]	1.24. f(x)=(x3/3)-4x-1; [-3; 1]

Задание №2. Провести полное исследование и построить график функции.

2.1.	2.2.
2.3.	2.4.
2.5.	2.6.
2.7.	2.8.
2.9.	2.10.
2.11.	2.12.
2.13.	2.14.
2.15.	2.16.
2.17.	2.18.
2.19.	2.20.
2.21.	2.22.
2.23.	2.24.

Задание №3. Провести полное исследование и построить график функции.

3.1. y=ln(x)/x	3.2. y=(2x+1)e-x
3.3. y=xex	3.4. (1/2)ln((x+1)/(x-1))
3.5. (1/2)ln((1+x)/(1-x))	3.6. y=xe-x
3.7. y=x/lnx	3.8. y=
3.9. y=x3e-x	3.10. y=x-ln(x+1)
3.11. y=(x2-1)/(x2+1)	3.12. y=x2/(x-1)
3.13. y=(4x3+5)/x	3.14. y=x4/(x3-1)
3.15. y=(2-4x2)/(1-4x2)	3.16. y=
3.17. y=x2-2lnx	3.18. y=e1/(2-x)
3.19. y=(2+x2)	3.20. y=(x-1)e3x+1
3.21. у=х2е-х	3.22. у=
3.23. у=(3х-2)е1-х	3.24. y=(x+2)2/(x+1)

Задание №4. 1) Вычислить приближенно значение функции z=f(x, y) в точке В, исходя из значения функции в точке А и заменив приращение функции дифференциалом.

2) Составить уравнение касательной плоскости к поверхности z=f(x, y) в точке А.

4.1. z=x2+xy+y2; A(1; 2); В(1,02; 1,96).	4.2. z=3x2-xy+x+y; A(1; 2); В(1,02; 1,96).
4.3. z=x2+3xy-6y; A(4; 1); В(3,96; 1,03).	4.4. z=x2-y2+6x+3y; A(2; 3); В(2,02; 2,97).
4.5. z=x2+2xy+3y2; A(2; 1); В(1,96; 1,04).	4.6. z=x2+y2+2x+y-1; A(2; 4); В(1,98; 3,91).
4.7. z=3x2+2y2-xy; A(-1; 3); В(-0,98; 2,97).	4.8. z=x2-y2+5x+4y; A(3; 3); В(3,02; 2,98).
4.9. z=2xy+3y2-5x; A(3; 4); В(3,04; 3,95).	4.10. z=xy+2y2-2x; A(1; 2); В(0,97; 2,03).
4.11. z=x2+xy+y2; A(2; 1); В(2,02; ,97).	4.12. z=2x2+3xy+y2; A(2; 2); В(2,03; 1,96).
4.13. z=5x2+6xy+x; A(1; 2); В(0,98; 2,02).	4.14. z=3x2+2xy+y2; A(-1; 2); В(-1,01; 2,03).
4.15. z=x2+3y2+x-2y; A(1; 2); В(1,03; 1,97).	4.16. z=x2+ y2+xy; A(1; 3); В(1,07; 2,93).
4.17. z=x2+2y2+x-y; A(3; 1); В(2,96; 1,04).	4.18. z=x2+3xy+y2-x; A(2; 3); В(2,03; 2,98).
4.19. z=x2+2xy-2y2+4x; A(2; 1); В(1,96; 1,03).	4.20. z=x2+xy+y2-x+2y; A(1; 3); В(1,04; 3,05).
4.21. ; A(3; 4); В(2,9; 4,2).	4.22. z=x2-6xy-y2; A(0; -2); В(-0,1; -1,9).
4.23. z=5x2-2xy-3y3; A(-2; 1); В(-1,9; 0,9).	4.24. ; A(4; 1); В(3,9; 1,05).

Задание №5. Найти наименьшее и наибольшее значения функции z=f(x, y) в замкнутой области D, заданной системой неравенств. Сделать чертеж области.

5.1. z=x2+y2-9xy+2;	5.2. z=x2+2y2;
5.3. z=-x2-y2-xy+3;	5.4. z=x2+3y2+x-y;
5.5. z=x2+2y2+2xy;	5.6. z=-x2-y2-xy+3;
5.7. z=-x2+2xy+10;	5.8. z=x2-y2+2xy+4x;
5.9. z=x2+xy-2;	5.10. z=x2+xy;
5.11. z=x2-2y2+4xy-6x-1;	5.12. z=x2+y3-3xy;
5.13. z=x2+y2-xy-4x;	5.14. z=x+y+xy;
5.15. z=2x3+y2+4x2-2xy;	5.16. z=x2+y2-xy-4x;
5.17. z=y2-2x+xy;	5.18. z=2xy+y2-4x;
5.19. z=x2+y2+2x+4y+1;	5.20. z=2x2+2y2+2xy;
5.21. z=x2-y2+2xy-8x;	5.22. z=x2+y2-4x;
5.23. z=2xy-y2-x;	5.24. z=x2+2y2+2xy+2x;

Задание №6. Найти уравнение касательной, нормальной плоскости и кривизну линии r=r(t) в точке t₀.

6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
6.8.
6.9.
6.10.
6.11.
6.12.
6.13.
6.14.
6.15.
6.16.
6.17.
6.18.
6.19.
6.20.
6.21.
6.22.
6.23.
6.24.

Раздел 4.

НЕОПРЕДЕЛЕННЫЙ И ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ.

1. Определение и свойства неопределенного интеграла.
Литература , гл. Х, §1-3, упр. 2, 5, 7, 9, 11, 14, 16, 17, 25, 41, 46, 49, 58. 60, 66.

2. Основные методы интегрирования.

Литература , гл. Х, §4, упр.27, 28, 33, 37, 47, 51, 65, 72, 83, 89, 91, 94, 100, 101; §6, упр. 127-131, 134, 135, 138, 140, 143, 145.

3. Стандартные методы интегрирования некоторых классов функций.
Литература , гл. Х, §5, упр. 102, 105, 107, 110, 112, 113, 115, 116, 123, 125; §7-9, упр. 156, 163, 164, 167, 169; §10, упр. 170, 176, 177; §12, упр. 196, 198, 203, 204, 209, 212, 214, 216; §13, упр. 178, 180; §14.

4. Определение, свойства и вычисления определенного интеграла.
Литература , гл. ХI, §1-5, §6 упр. 8, 10, 11, 13, 16-21, 23, 24.

5. Несобственные интегралы.

Литература , гл. Х, §7, упр. 29-31, 34, 35, 37-40.

6. Геометрические приложения определенного интеграла.
Литература , гл. ХII, §1, упр. 1, 3, 5-11; §2, упр. 13, 14, 17, 18; §3, упр. 38-41, 43, 47; §4, 5, упр. 20-23, 25, 32; §6, упр. 49, 51, 53, 56.

Вопросы для самопроверки.

1. Дайте определения:

- первообразной функции;

- неопределенного интеграла.

2. Напишите таблицу основных интегралов.

3. Докажите свойства неопределенного интеграла.

4. Выведите формулу замены переменной в неопределенном интеграле.

5. Выведите формулу интегрирования по частям в неопределенном интеграле. Какие типы интегралов целесообразно брать этим методом?

6. Интегрирование простейших дробей I, II, III, IV типов.

7. Изложите правило разложения правильной рациональной дроби на простейшие. Продемонстрируйте его на примерах.

8. Как интегрируются рациональные дроби?

9. Изложите методы нахождения интегралов вида:
а) ;

в) ,

где p, q,…, r – рациональные числа, R – рациональная функция.
Приведите примеры.

10. В чем состоит общая идея метода рационализации при интегрировании иррациональных и трансцендентных функций?

11. Дайте определение определенного интеграла и укажите его геометрический смысл.

12. Докажите основные свойства определенного интеграла:
а) ;

б) ;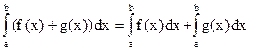

в) .

13. Сформулируйте свойства определенного интеграла, выражающиеся с помощью неравенств.

14. Докажите теорему о среднем значении для определенного интеграла. В чем ее геометрический смысл?

15. Докажите, что является первообразной для f(x) (теорема Барроу).

16. Выведите формулу Ньютона-Лейбница.

17. Выведите формулу замены переменной в определенном интеграле. Приведите пример.

18. Докажите формулу интегрирования по частям для определенного интеграла.

19. Дайте определения:

- несобственного интеграла первого рода;

- несобственного интеграла второго рода.

20. Когда говорят, что несобственный интеграл первого (второго) рода сходится или расходится? Приведите примеры сходящихся и расходящихся интегралов первого (второго) родов.

21. Сформулируйте необходимый и достаточный признак сходимости несобственных интегралов первого (второго) рода.

22. Сформулируйте общий и частный признаки сравнения несобственных интегралов первого (второго) рода. Как используются они для установления сходимости или расходимости несобственных интегралов?

23. Напишите формулу для вычисления площади криволинейной трапеции, ограниченной кривой, заданной в декартовой системе координат.

24. Выведите формулу для вычисления площади криволинейного сектора, ограниченного кривой, заданной в полярной системе координат.

25. Напишите формулу для вычисления площади фигуры, когда линии, ее ограничивающие, представлены параметрическими уравнениями.

26. Выведите формулу для вычисления длины дуги кривой, заданной:
- параметрическими уравнениями;

- уравнениями в декартовой системе координат;

- уравнениями в полярной системе координат.

27. выведите формулу для вычисления объема тела по известным площадям поперечных сечений.

28. Как вычисляются с помощью определенного интеграла объем тела вращения:

- ось вращения – ось ОХ;

- ось вращения – ось ОУ.

Во многих случаях задачу интегрирования можно свести, используя специальные методы, к нахождению интегралов, составляющих таблицу интегралов:

(I)

(II)

(III)

(IV)

(V)

(VI)

(VII)

(VIII)

(IX)

(X)

(XI)

(XII)

(XIII)

Пример. Вычислить неопределенные интегралы:

а) ; б) ; в) .

Решение.

а) Так как

,

то интеграл преобразуется к виду

.

Применим к нему формулу (II)

.

б) Применим формулу интегрирования по частям:

.

Так как , то обозначив u=x, , найдем . Следовательно,

.

Второе слагаемое найдем по таблице (формула (XII)). Получим

.

в) Подынтегральная функция является рациональной алгебраической дробью. Так как дробь неправильная (степень числителя больше степени знаменателя), то ее можно записать в виде суммы многочлена и правильной рациональной дроби. Найдя их, применив алгоритм деления «столбиком»:

_
	х

Значит,

.

Разложение дробной части на простейшие дроби имеет вид:

.

Следовательно,

.

Решив систему уравнений:

,

получим А=2, В=3, С=2. Осталось найти:

.

По формуле III и VI находим

.

Окончательно получим:

Контрольные задания

1. Вычислить неопределенные интегралы. В пункте а) результаты проверить дифференцированием.

1.1. а) ; б) ; в) ;

1.2. а) ; б) ; в) ;

1.3. а) ; б) ; в) ;

1.4. а) ; б) ; в) ;

1.5. а) ; б) ;в) ;

1.6. а) ; б) ; в) ;

1.7. а) ; б) ; в) ;

1.8. а) ; б) ; в) ;

1.9. а) ; б) ; в) ;

1.10. а) ; б) ; в) ;

1.11. а) ; б) ; в) ;

1.12. а) ; б) ; в) ;

1.13. а) ; б) ; в) ;

1.14. а) ; б) ; в) ;

1.15. а) ; б) ; в) ;

1.16. а) ; б) ; в) ;

1.17. а) ; б) ; в) ;

1.18. а) ; б) ; в) ;

1.19. а) ; б) ; в) ;

1.20. а) ; б) ; в) ;

1.21. а) ; б) ; в) ;

1.22. а) ; б) ; в) ;

1.23. а) ; б) ; в) ;

1.24. а) ; б) ; в) .

2. Вычислить определенные интегралы.

2.1. ; 2.2. ;

2.3. ; 2.4. ;

2.5. ; 2.6. ;

2.7. ; 2.8. ;

2.9. ; 2.10. ;

2.11. ; 2.12. ;

2.13. ; 2.14. ;

2.15. ; 2.16. ;

2.17. ; 2.18. ;

2.19. ; 2.20. ;

2.21. ; 2.22. ;

2.23. 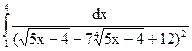; 2.24. .

3.1. ; 3.2. ; 3.3. ;

3.4. ; 3.5. ; 3.6. ;

3.7. ; 3.8. ; 3.9. ;

3.10. ; 3.11. ; 3.12. ;

3.13. ; 3.14. ; 3.15. ;

3.16. ; 3.17. ; 3.18. ;

3.19. ; 3.20. ; 3.21. ;

3.22. ; 3.23. ; 3.24. .

4. Вычислить несобственные интегралы или установить их расходимость.

4.1. ; 4.2. ; 4.3. ;

4.4. ; 4.5. ; 4.6. ;

4.7. ; 4.8. ; 4.9. ;

4.10. ; 4.11. ; 4.12. ;

4.13. ; 4.14. ; 4.15. ;

4.16. ; 4.17. ; 4.18. ;

4.19. ; 4.20. ; 4.21. ;

4.22. ; 4.23. ; 4.24. .

5.1. Вычислить площадь фигуры, ограниченной параболой и прямой .

5.2. Вычислить площадь фигуры, ограниченной графиками функций ,

5.3. Вычислить площадь фигуры, ограниченной одной аркой циклоиды , и осью ОХ.

5.4. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями:

5.5. Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах

5.6. Вычислить площадь фигуры, ограниченной четырехлепестковой розой .

5.7. Вычислить длину дуги кривой, заданной уравнениями в декартовой системе координат .

5.8. Вычислить длину дуги полукубической параболы от точки А(2; 0) до точки В(6; 8).

5.9. Вычислить длину дуги кривой, заданной параметрическими уравнениями:

5.10. Вычислить длину одной арки циклоиды .

5.11. Вычислить длину дуги кривой, заданной уравнениями в полярных координатах

.

5.12. Вычислить длину кардиоиды .

5.13. Вычислить объем тела, образованного вращением вокруг оси ОУ фигуры, ограниченной кривыми .

5.14. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами .

5.15. Вычислить объем тела, ограниченного поверхностями ;

.

5.16. Найти площадь фигуры, ограниченной кардиоидой и окружностью .

5.17. Найти площадь фигуры, ограниченной полукубической параболой , прямой у=8 и осью ОУ.

5.18. Найти площадь фигуры, ограниченной кривой и осями координат.

5.19. Найти площадь фигуры, ограниченной окружностями и .

5.20. Вычислить длину дуги кривой от до .

5.21. Найти площадь фигуры, ограниченной параболой и прямой .

5.22. Найти площадь фигуры, ограниченной кардиоидой и окружностью .

5.23. Найти длину одной арки циклоиды .