Статистичні характеристики диференціації та концентрації.

Коефіцієнти варіації, їх роль у статистичному аналізі.

Варіацією ознаки називають різницю у числових зна­ченнях ознак одиниць сукупності та їх коливання навколо сере­дньої величини, що характеризує сукупність. Чим менша варіа­ція, тим одноріднішою є сукупність і більш надійною (типовою) є середня величина.

До основних абсолютних і відносних показників, що ха­рактеризують варіацію, є такі: розмах варіації; середнє лінійне відхилення; дисперсія; середнє квадратичне відхилення; коефі­цієнт варіації тощо.

Розмах варіації - це різниця між найбільшим та най­меншим значеннями ознаки.

Величина показника залежить тільки від крайніх значень ознаки і не враховує всіх значень, що містяться між ними.

Досконалішим є визначення варіації через інші показни­ки, які дають змогу усунути недолік розмаху варіації.

Середнє лінійне відхилення являє собою середню ариф­метичну з абсолютних значень усіх відхилень індивідуальних значень ознаки від середньої.

Наявність абсолютних значень відхилень від середньої пояснюється так: середня арифметична має нульову властивість, згідно якої сума відхилень від середньої індивідуальних значень ознаки зі своїми знаками дорівнює нулю; щоб мати суму всіх відхилень, відмінних від нуля, кожне з них слід брати за абсо­лютною величиною.

Основним недоліком середнього лінійного відхилення є те, що в ньому не враховуються знаки відхилень, тобто їх спря­мованість. Тому цей показник варіації використовується рідко (аналіз складу працюючих, ритмічність виробництва, обертання коштів у зовнішній торгівлі тощо). Показниками варіації, які б усунули недоліки середнього лінійного відхилення, є дисперсія та лінійне квадратичне відхилення.

Дисперсією називають середню арифметичну квадратів відхилень індивідуальних значень ознаки. В залежності від ви­хідних даних дисперсія може обчислюватись за формулами се­редньої арифметичної простої або зваженої.

Дисперсія - це один з найбільш розповсюджених в еко­номічній практиці узагальнюючих показників розміру варіації у сукупності. Дисперсію використовують не лише для оцінки ва­ріації, а й для вимірювання зв'язків між досліджувальними фак­торами; розклад дисперсії на складові дозволяє оцінити вплив різних факторів, які обумовлюють варіацію ознаки.

Середнє квадратичне відхилення, як і дисперсія, висту­пає в якості широко використовуємого узагальнюючого показ­ника варіації.

Смислове значення середнього квадратичного відхилен­ня таке саме, як і лінійного відхилення: воно показує, на скільки в середньому відхиляються індивідуальні значення ознаки від їх середнього значення. Перевага цього показника порівняно із середнім лінійним відхиленням полягає у відсутності умовного припущення з підсумування відхилень без врахування їх знаків, бо відхилення використовуються у квадратній степені. Крім за­значеного, перевагою даного показника у зрівнянні з дисперсією є те, що середнє квадратичне відхилення виражається в тих же одиницях вимірювання, що і значення досліджувальної ознаки (грн, кг, га тощо). Тому цей показник називають також станда­ртним відхиленням.

Коефіцієнтом варіації називають процентне відношення середнього квадратичного відхилення до середньої арифметич­ної величини ознаки.

Чим більше коефіцієнт варіації, тим менш однорідна су­купність і тим менш типова середня для даної сукупності. Вста­новлено, що сукупність кількісно однорідна, якщо коефіцієнт варіації не перевищує 33%.

Дисперсія посідає особливе місце у статичному аналізі соціально-економічних явищ і є важливим елементом статисти­чних методів, зокрема у дисперсному аналізі.

Статистичні характеристики диференціації та концентрації.

Ступінь нерівномірності розподілу досліджуваної ознаки, не пов’язаний ні з обсягом сукупності, ні з чисельністю окремих груп, називають концентрацією. При дослідженні нерівномірності розподілу досліджуваної ознаки за територією поняття “концентрація” замінюють поняттям “локалізація”.Централізація означає зосередженість (скупченість) обсягу ознаки у окремих одиниць (наприклад, капіталу в окремих комерційних банках, продукції якогось виду на окремих підприємствах і т. ін.).

Узагальнюючий показник централізації І_Z розраховується за формулою:

,

де m_i – значення ознаки і-ої одиниці сукупності;

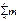- обсяг ознаки всієї сукупності;

n - обсяг сукупності (кількість одиниць, що входять у сукупність).

Коефіцієнт концентрації (коефіцієнт Лоренца)є узагальнюючою для сукупності характеристикою відхилення розподілу від рівномірного і визначається за формулою:

.

Чим ближче значення цього показника до 1 (100%), тим вищий рівень концентрації, при значенні К=0 розподіл ознаки за всіма одиницями сукупності є рівномірним. При визначенні цього коефіцієнта можна оперувати як частками одиниці, так і відсотками. Порівняння структур на основі відхилень часток дозволяє вимірювати диференціацію сукупності за даними інтервальних рядів із нерівними інтервалами та атрибутивних рядів розподілу.

Оцінка рівня концентрації при вивченні економічних явищ дуже часто здійснюється по кривій концентрації Лоренца. Для її побудови необхідно мати частотний розподіл одиниць досліджуваної сукупності та відповідний до нього частотний розподіл ознаки, що вивчається. При цьому для зручності розрахунків і підвищення рівня аналітичності даних одиниці сукупності, як правило, розбиваються на рівні групи – 10 груп по 10% одиниць в кожній групі, або – 5 груп по 20% одиниць і т.д.