Тема 2. Классическое определение вероятности

Тема 1. Основные понятия теории вероятностей

Основные понятия по теме:

1. Испытание, элементарный исход, исход испытания, событие.

2. Достоверное событие, невозможное событие, случайное событие.

3. Совместные события, несовместные события, равносильные события, равновозможные события, единственно возможные события.

4. Полная группа событий, противоположные события.

5. Элементарное событие, составное событие.

6. Сумма нескольких событий, произведение нескольких событий. Их геометрическая интерпретация

Применение всех этих понятий на практических примерах.

Примерные тестовые задания, предлагаемые в этой теме:

1. В задаче « Производится два выстрела по мишени. Найти вероятность того, что мишень будет поражена один раз» испытанием является:

1)* производится два выстрела по мишени;

2) мишень будет поражена один раз;

3) мишень будет поражена два раза.

2. Бросают монету. Событие: А – «выпадет герб». Cобытие 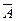– «выпадет цифра» является:

1) случайным;

2) достоверным;

3) невозможным;

4)* противоположным.

3. Подбрасывается игральный кубик. Обозначим события: А — «выпадение 6 очков», В — «выпадение 4 очков», D — «выпадение 2 очков», С — «выпадение четного числа очков». Тогда событие С равно

1) ;

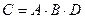2) ;

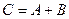3)* ;

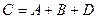4) .

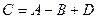4. Студент должен сдать два экзамена. Событие А — « студент сдал первый экзамен», событие В — «студент сдал второй экзамен», событие С — «студент сдал оба экзамена». Тогда событие С равно

1)* ;

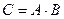2) ;

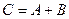3) ;

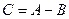4) .

5. Из букв слова «ЗАДАЧА» наугад выбирается одна буква. Событие — «выбрана буква К» является

1) случайным;

2) достоверным;

3)* невозможным;

4) противоположным.

6. Из букв слова «МИР» наугад выбирается одна буква. Событие — «выбрана буква М» является

1)* случайным;

2) достоверным;

3) невозможным.

7. Событие — «из урны, содержащей только белые шары, извлекают белый шар» является

1) случайным;

2)* достоверным;

3) невозможным.

8. Два студента сдают экзамен. События: А — «экзамен сдаст первый студент», В — «экзамен сдаст второй студент» являются

1) несовместными;

2) достоверными;

3) невозможными;

4)*совместными.

9. События называют несовместными, если

1) наступление одного не исключает возможность появления другого;

2) при осуществлении комплекса условий каждое из них имеет равную возможность наступить;

3) при испытании обязательно наступит хотя бы одно из них;

4)* наступление одного исключает возможность появления другого.

10. События называют единственно возможными, если

1) наступление одного не исключает возможность появления другого;

2) при осуществлении комплекса условий каждое из них имеет равную возможность наступить;

3)* при испытании обязательно наступит хотя бы одно из них;

4) наступление одного исключает возможность появления другого.

Тема 2. Классическое определение вероятности

Основные понятия по теме:

1. Вероятность события, классическое определение вероятности случайного события.

2. Исход, благоприятствующий событию.

3. Геометрическое определение вероятности.

4. Относительная частота события.

5. Статистическое определение вероятности.

6. Свойства вероятности.

7. Способы подсчета числа элементарных исходов: перестановки, сочетания, размещения.

Применение всех этих понятий на практических примерах.

Примерные тестовые задания, предлагаемые в этой теме:

1. События называют равновозможными, если

1) они несовместны;

2)* при осуществлении комплекса условий каждое из них имеет равную возможность наступить;

3) при испытании обязательно наступит хотя бы одно из них;

4) наступление одного исключает возможность появления другого.

2. Испытание — «бросают две монеты». Событие — «хотя бы на одной из монет выпадет герб». Число элементарных исходов, благоприятствующих данному событию равно:

1) одно;

2) два;

3)* три;

4) четыре.

3. Испытание — «бросают две монеты». Событие — «на одной из монет выпадет герб». Число всех элементарных, равновозможных, единственно возможных, несовместных исходов равно:

1) одно;

2) два;

3) три;

4)* четыре.

4. В урне 12 шаров, ничем, кроме цвета, не отличающихся. Среди этих шаров 5 черных и 7 белых. Событие — «случайным образом извлекают белый шар». Для этого события число благоприятствующих исходов равно:

1) 12;

2) 5;

3) *7;

4) 1.

5. В урне 12 шаров, ничем, кроме цвета, не отличающихся. Среди этих шаров 5 черных и 7 белых. Событие — «случайным образом извлекают белый шар». Для этого события число всех исходов равно:

1) *12;

2) 5;

3) 7;

4) 1.

6. Вероятность события принимает любое значение из промежутка:

1) (-1; 1);

2) ( 0; 1);

3) ;

4) ;

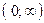5)* .

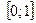7. Абонент забыл две последних цифры телефонного номера и, зная, лишь, что они различны, набрал их наудачу. Сколькими способами он это может сделать?

1) ;

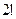2)* ;

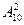3) ;

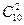4) ;

5) .

8. Сколькими способами можно пересадить 5 человек?

1) 5;

2) ;

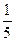3) ;

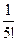4)* .

9. В студенческой группе, состоящей из 10 человек, нужно выбрать двух человек на конференцию. Сколькими способами это можно сделать?

1) ;

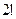2) ;

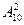3) * ;

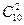4) ;

5) .

10. Дана задача: «В круг вписан треугольник. В круг наудачу брошена точка. Какова вероятность того, что эта точка попадет в треугольник?» Для решения этой задачи необходимо использовать

1) классическое определение вероятности;

2)*геометрическое определение вероятности;

3) формулу Бернулли;

4) формулу Бейеса.