Тема: Алгебраїчні вирази, рівняння, системи рівнянь.

Рекомендована література

Базова

1. Бевз Г. П. Методика викладання математики: Навч. посібник. − К.: Вища шк.., 1989. − 367 с.

2. Василевский А. Б. Обучение решению задач: Учеб. пособие для вузов. − Мн.: Высш. школа, 1979. − 192 с.

3. Жовнір Я. М., Євдокимов В. І. 500 задач з методики викладання математики: Навч. посібник. − Х.: Основа, 1997. − 392 с.

4. Задачи повышенной трудности по алгебре и началам анализа: Учеб. пособие для 10-11 кл. сред.шк./Б. М. Ивлев, А. М. Абрамов, Ю. П. Дудницын, С. И. Шварцбурд. − М.: Просвещение, 1990. − 48 с.

5. Кострикина Н. П. Задачи повышенной трудности в курсе математики 4-5 классов: Кн. для учителя. − М.: Просвещение, 1986. −96 с.

6. Кострикина Н. П. Задачи повышенной трудности в курсе алгебры 7-9 классов: Кн. для учителя. − М.: Просвещение, 1991. −239 с.

7. Кушнир И. Шедевры школьной математики. Задачи с решениями в двух книгах. − К.: Астарта, 1995

8. Литвиненко В. Н., Мордкович А. Г. Практикум по элементарной математике: Алгебра. Тригонометрия: Учеб. пособие для студентов физ. - мат. спец. пед. ин-тов. − М.: Просвещение, 1991. − 352 с.

9. Методика преподавания математики в средней школе: Общая методика. Учебное пособие для студентов физ.-мат. фак. пед.ин-тов/ В. С. Оганесян, Ю. М. Колягин, Г. А. Луканкин, В. Я. Саннинский. − М.: Просвещение, 1980. − 368 с.

10. Методика преподавания математики в средней школе: Общая методика. Учебное пособие для студентов пед. ин-тов /А. Я. Блох, Е. С. Канин, Н. Г. Килина и др.; Сост. Р. С. Черкасов, А. А. Столяр. − М.:Просвещение, 1985. − 336 с.

11. Носенко Ю. А. Математика. Посібник для реалізації стиковочного курсу математики та для підготовки до вступних випробувань. − Донецьк: РВА ДонНТУ, 2003. − 2002 с.

12. Пойа Д. Как решать задачу. − М., 1961. − 207 с.

13. Пойа Д. Математика и правдоподобные рассуждения. − М.: Наука, 1975. − 464 с.

14. Пойа Д. Математическое открытие. − М.: Наука, 1976, − 448 с.

15. Ігначкова А. В., Малярець Л. М. Математика для абітурієнтів: Навчальний посібник. − Х.: Видавничий дім „ІНЖЕК”, 2003. − 550 с.

16. Фридман Л. М., Турецький Е. Н. Как научиться решать задачи : Пособие для учащихся. − М.: Просвещение, 1987. −175 с.

17. Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учеб. пособие для 10 кл. серед.шк. − М.: Просвещение, 1989. −252 с.

18. Шарыгин И. Ф., Голубев В. И. Факультативный курс по математике: Решение задач: Учеб. пособие для 11 кл. cред. шк. − М.: Просвещение, 1991. −384с.

19. Ясінський В. В. Математика. Методичний посібник для слухачів ІДП НТУУ „КПІ” /За редакцією В.С. Мельника. − К.: НТУУ „КПІ”, 2003. − 324 с.

Тематика та зміст практичних занять.

Практичне заняття №1-2.

Тема: Текстові задачі.

1. Три комбайнери зібрали хліб з 1290 га. Кількості робочих днів цих комбайнерів відносилися між собою як 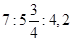, кількість робочих годин в день були обернено пропорційні числам 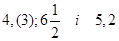.Скільки гектарів зібрав кожний комбайнер? (6.13)

2. Якщо двічі послідовно підвищувати ціну товару А на одне і те саме число р%, то нова ціна товару буде на 28% вища за ціну товару В. Якщо двічі послідовно зменшувати ціну товару В на р%, то нова ціна товару В буде на 68% нижче ціни товару А. Знайти число р і відношення первісних цін товарів А і В. (6.56)

3. За А% загальної кількості товару одержали р% прибутку. З яким процентом прибутку треба продавати решту товару, щоб загальний прибуток становив r%? (6.59)

4. Відомо, що протягом року вклад в комерційному банку зростає на певний процент, що визначається кожним банком окремо. На початку року чверть всіх грошей поклали в перший банк, а решту − в другий. Наприкінці першого року сума цих вкладів досягла 470 грн., а наприкінці наступного року − 553 грн. Було підраховано, що якби спочатку чверть вихідної суми поклали в другий банк, а решту − в перший банк, то наприкінці першого року сума вкладів в цих банках дорівнювала б 450 грн. Визначити, яка в цьому випадку була б сума вкладів в цих банках наприкінці другого року? (6.64)

5. П’ятеро робітників виконують деяку роботу. Перший, другий і третій, працюючи разом, можуть виконати роботу за 7,5 год; перший, третій і п’ятий − за 5 год; перший, другий і четвертий − за 6 год, а другий, четвертий і п’ятий − за 4 год. За який час виконують цю роботу всі п’ятеро робітників, працюючи разом? (6.71)

6. У басейн проведено 4 труби. Через першу, другу і третю труби заповнюється за 12 хв; через другу, третю і четверту труби − за 15 хв; а через першу і четверту − за 20 хв. За який час наповниться басейн через чотири труби? (6.72)

7. Дві молотарки обмолочують весь хліб за а днів. Якби перша молотарка обмолотила половину всього хліба, а друга − решту, то вони працювали б b днів. За скільки днів кожна молотарка окремо може обмолотити весь хліб? (6.82)

8. Маємо три сплави. Перший сплав містить 55% хрому і 45% нікелю, другий − 60% нікелю, 25% хрому і 15% кобальту, третій − 70% хрому і 30% кобальту. З них треба приготувати новий сплав, який містив би 20% кобальту. Які значення може приймати процентний вміст нікелю в цьому новому сплаві? (6.95)

9. У залі поставлені стільці в 13 рядів, причому на останній ряд стільців не вистачило. Тому їх переставили в 27 рядів, причому в кожному ряді поставили на 7 стільців менше, ніж при початковому розставленні, і на останній ряд не вистачило 3 стільців. Скільки всього було стільців? (6.132)

10. У домашній бібліотеці кількість художніх книг в чотири рази більша кількості наукових книг, а кількість дитячих книг кратна кількість наукових. Якщо кількість дитячих книг збільшити в 5 разів, то їх стане на 22 більше, ніж художніх. Скільки книг було в бібліотеці, якщо відомо, що їх було не менше 100? (6.133)

11. Добуток двозначного числа на число, записане тими самими цифрами, але в оберненому порядку, дорівнює 1008. Знайти це двозначне число.(6.140)

12. На яке ціле додатне число треба поділити число 287, щоб остача становила 20% від частки? (6.161)

13. На яке ціле двоцифрове число треба помножити число 41, щоб дістати число, сума цифр якого дорівнює 40% від шуканого числа? (6.163)

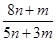14. Натуральні числа m і n утворюють нескоротний дріб . На які натуральні числа можна скоротити дріб , коли відомо, що він скорочується? (6.164)

15. Підприємство випускає телевізори і є прибутковим. Відомо, що при виготовленні n телевізорів в місяць витрати підприємства на випуск одного телевізора складають не менше 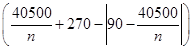грн., а ціна реалізації кожного телевізора при цьому не перевищує 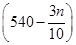грн.. Визначити такий щомісячний обсяг виробництва телевізорів, при якому може бути одержано найбільший щомісячний прибуток. (6.176)

Практичне заняття №3.

Тема: Прогресії.

1. Всі сторони та висота трапеції складають арифметичну прогресію. Периметр трапеції дорівнює 40 см, площа трапеції 55 см ² . Знайти сторони та висоту трапеції. (7.18)

2. Батько дарує кожному з своїх п’яти синів на день народження , починаючи з п’яти років, стільки книжок, скільки сину років. Роки утворюють арифметичну прогресію, різниця якої дорівнює 3. Скільки років кожному сину, коли утворилась бібліотека з 325 книжок? (7.19)

3. Два тіла, вийшовши одночасно рухаються на зустріч один одному з двох пунктів, відстань між якими 200 м. Перше тіло проходить 12 м/с, а друге тіло пройшло в першу секунду 20 м і кожну наступну секунду проходить на 2 м менше, ніж в попередню. Через скільки секунд тіла зустрінуться? (7.20)

4. Кути випуклого многокутника утворюють арифметичну прогресію: 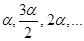.Знайти кути такого многокутника з найбільшим можливим числом сторін. (7.21)

5. При яких значеннях параметра 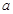знайдуться такі значення 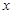, що числа 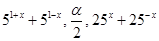будуть утворювати арифметичну прогресію?(7.23)

6. Дві арифметичні прогресії мають однакове число членів. Відношення останнього члена першої прогресії до першого члена другої прогресії дорівнює відношенню останнього члена другої прогресії до першого члена першої й дорівнює 4. Відношення суми першої прогресії до суми другої дорівнює 2. Знайти відношення різниці першої прогресії до різниці другої. (7.33)

7. Знайти тризначне число, якщо його цифри утворюють геометричну прогресію, а цифри числа, яке менше даного на 400, - утворюють арифметичну прогресію. (7.75)

8. Бак наповнювали бензином протягом цілого числа годин, причому відношення кількості бензину, що наливали за кожну наступну годину, до кількості бензину, що наливали за попередню годину, є величина стала. За годину до наповнення в баці виявилося 372 л. Якщо з повного баку вилити ту кількість бензину, яка поступила за першу годину, то в ньому залишилось 186 л.; якщо потім із нього додатково вилити ту кількість бензину, що була налита за другу, останню та передостанню годину разом, то в баці залишилось 72 л. Скільки бензину поступило у бак за першу годину?

9. Кути 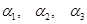лежать в першій чверті та утворюють арифметичну прогресію з різницею 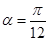, а їх тангенси утворюють геометричну прогресію. Знайти ці кути.

Практичне заняття №-4-5.

Тема: Алгебраїчні вирази, рівняння, системи рівнянь.

1. Довести, що якщ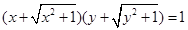о , то .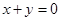

2. Визначити чисельне значення виразу .

3. Довести, що не існує цілих чисел 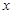і 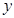таких, які б задовольняли рівнянню .

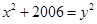4. Знайти усі пари простих чисел 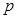і 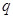, що задовольняють рівності .

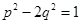5. Розв’язати рівняння 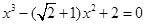(ХНЕУ).

6. Розв’язати рівняння 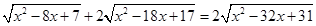(ХНЕУ).

7. Розв’язати рівняння .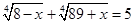

8. Розв’язати рівняння .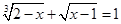

9. Розв’язати рівняння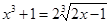

10. Розв’язати рівняння 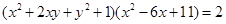(ХНЕУ).

11. Побудувати графік рівняння .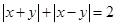

12. Розв’язати рівняння .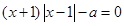

13. Розв’язати рівняння . (КПІ)

14. Розв’язати рівняння 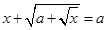. (КПІ)

15. Розв’язати систему рівняння 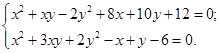(Ін. шт. інтелекту)

16. Знайти всі значення а, при яких система має хоча б один розв’язок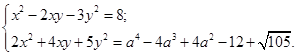

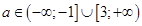
17. Розв’язати рівняння 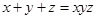в натуральних числах. (ХНУ ім. Каразіна)

18. Знайти всі цілочислені розв’язки рівняння .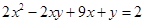

Практичне заняття №6-7.

Тема: Тригонометрія.

1. Чи існує таке число х, що значення виразів 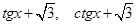– цілі числа?

2. Знайти 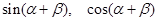, якщо 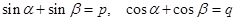. (ХНУР)

3. Обчислити 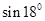(ХНУР).

4. Показати, що 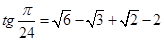. (ХНУ ім. Каразіна)

5. Довести, що 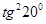є коренем рівняння 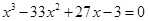. (ХНУ ім. Каразіна)

6. Знайти 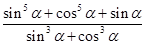, якщо .

7. Обчислити .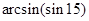

8. Обчислити .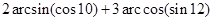

9. Обчислити (без таблиці і калькулятора) .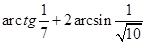

10. Спростити вираз: 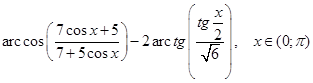. (ХНУ ім. Каразіна)

11. Розв’язати рівняння 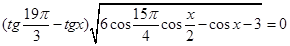. (МАН).

12. Знайдіть усі числа 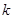, при яких рівняння 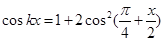має розв’язки. Знайдіть ці розв’язки.

13. Розв’язати рівняння 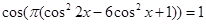. (КПІ)

14. Розв’язати рівняння .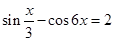

15. Розв’язати рівняння .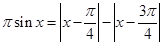

16. Розв’язати рівняння .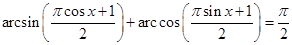

17. Знайти всі значення параметра а, при кожному з яких рівняння має розв’язки. Знайти ці розв’язки 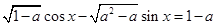. (КПІ)

18. Знайти дійсні значення параметра а, при кожному з яких рівняння має єдиний розв’язок на вказаному проміжку .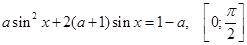

19. Знайти всі значення параметра а, при кожному з яких для всіх 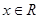виконується нерівність 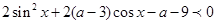. (КПІ)

20. Знайти всі значення параметра а, при кожному з яких система рівнянь має розв’язки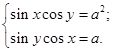

Практичне заняття. № 8.