Основные теоремы теории вероятностей

Суммой A+B событий A и B называют событие, состоящее в появлении события A, или события B, или обоих этих событий.

Произведением 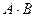событий A и B называют событие, состоящее в совместном появлении этих событий.

Условной вероятностью P(A|B) называют вероятность появления события A, найденная при условии, что событие B уже произошло.

Формула умножения вероятностей. Для любых событий A и B вероятность их произведения вычисляют по формуле P(AB)=P(A)P(B|A)=P(B)P(A|B).

Независимыми называют события (испытания), если появление одного из них не изменяет вероятности других. Если события A и B независимы, то вероятность их произведения вычисляют по формуле P(AB)=P(A)P(B).

Формула сложения вероятностей. Для любых событий A и B вероятность их суммы вычисляют по формуле P(A+B)=P(A)+P(B) – P(AB).

Несовместными событиями A и B называют события, если появление одного из них исключает появление другого события в одном и том же испытании. Если события A и B несовместны, то P(AB)=0 и P(A+B)=P(A)+P(B).

Противоположным событию A называют событие 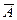, если оно несовместно с событием A и вместе с ним образует достоверное событие: A+ 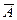=Ω, P(A)+P( 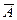)=1.

Формула полной вероятности. Вероятность события , которое наступит лишь при условии появления одного из несовместных событий H₁, H₂, …, H_n, образующих полную группу, вычисляют по формуле P(A)= (H_i)P(A|H_i). Так как неизвестно, какое из событий H₁, H₂, …, H_n приводит к появлению события A, поэтому события H₁, H₂, …, H_n называют гипотезами.

Формула Байеса (формула проверки гипотез). Пусть дана полная группа несовместных событий H₁, H₂, …, H_n и некоторое событие A. Тогда вероятность события H_k (k=1,2,…,n) при условии, что событие A произошло, вычисляют по формуле

Пример 1. Вероятность попадания в мишень одного стрелка равна 0,8, второго – 0,6. Стрелки независимо друг от друга сделали по одному выстрелу. Какова вероятность попадания в мишень хотя бы одного стрелка?

Решение. Первый способ. Событие A₁ – попадание в мишень первого стрелка. Вероятность этого события P(A₁) равна 0,8. Событие A₂ – попадание в мишень второго стрелка. P(A₂)=0,6. Необходимо вычислить вероятность события A₁+A₂ – попадание в мишень хотя бы одного стрелка (или первого, или второго, или обоих). По формуле сложения вероятностей P(A₁+A₂)=P(A₁)+P(A₂)–P(A₁A₂). По условию стрелки сделали выстрелы независимо друг от друга, то есть P(A₁A₂)=P(A₁)P(A₂) В результате искомая вероятность равна

P(A₁)+P(A₂)–P(A₁A₂)=0,8+0,6– 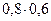=0,92.

Второй способ. Для события A₁ противоположным является событие – промах первого стрелка. Вероятность этого события P( ) равна 1–P(A₁). Противоположным событию A₂ является событие – промах второго стрелка. P( )=1–P(A₁). Противоположным событию A₁+A₂ является событие – промах одновременно и первого, и второго стрелков. Вероятность события A₁+A₂ можно вычислить следующим образом:

P(A₁+A₂)=1–P( )=1–P( )P( )=1–(1–P(A₁))(1–P(A₂)).

Искомая вероятность равна: P(A₁+A₂)=1–(1–0,8)(1–0,6)=0,92.

Третий способ. Можно представить событие A₁+A₂ как сумму событий: A₁A₂ – попадание в мишень и первого, и второго стрелков; A₁ – попадание в мишень первого стрелка и промах второго; A₂ – попадание в мишень второго стрелка и промах первого. Эти три события являются несовместными, тогда вероятность суммы этих событий равна сумме вероятностей каждого из них:

P(A₁+A₂)= P(A₁A₂+ A₂+ A₁ )= P(A₁A₂)+ P( A₂)+ P(A₁ ).

По условию события , независимы, то есть:

P(A₁+A₂)=P(A₁)P(A₂)+P(A₂)P( )+P(A₁)P( ).

В результате: P(A₁+A₂)= =0,92.

Ответ: 0,92.

Пример 2. В соревнованиях по бегу принимают участие две команды первокурсников и одна команда второкурсников. В каждой команде первокурсников пять юношей и три девушки, а в команде второкурсников – четыре юноши и четыре девушки. Для участия в забеге по жеребьевке выбрали одну из команд, из нее одного человека. а) Какова вероятность того, что выбран юноша? б) Выбран юноша. Какова вероятность того, что он первокурсник?

Решение. а) Нужно найти вероятность события A – выбран юноша. Вероятности событий: H₁ – выбрана команда первого курса; H₂ - выбрана команда второго курса; A|H₁ – выбран юноша при условии, что выбрана команда первого курса; A|H₂ – выбран юноша при условии, что выбрана команда второго курса соответственно равны 2/3; 1/3; 5/8; 1/2. По формуле полной вероятности:

P(A)= 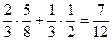≈0,58.

б) Вероятность события H₁|A – выбрана команда первого курса при условии, что выбран юноша – можно найти по формуле Байеса:

P(H₁|A)= 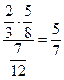≈0,7.

Ответ: 0,58; 0,7.

Упражнения.

7.3.1. Найдите вероятность того, что дни рождения двух друзей не приходятся на один месяц года. Ответ: 11/12.

7.3.2. В двух ящиках находится соответственно пять белых, одиннадцать черных, восемь красных и десять белых, восемь черных, шесть красных шаров. Из каждого ящика наудачу извлекают по одному шару. Какова вероятность, что оба шара одного цвета? Ответ: 0,323.

7.3.3. В коробке находятся четыре ампулы с препаратом А и десять – с препаратом В. Какова вероятность того, что две наудачу выбранные ампулы содержат один и тот же препарат? разные препараты? Ответ: 0,56; 0,44.

7.3.4. Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятность того, что при возгорании сработает первый и второй датчик соответственно равны 0,9 и 0,95. Найдите вероятность того, что при пожаре сработают: а) оба датчика; б) только один; в) хотя бы один. Ответ: 0,855; 0,14; 0,995.

7.3.5. Стрелок производит три выстрела по мишени. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны 0,4; 0,5; 0,7. Найдите вероятность того, что в результате этих выстрелов окажется: а) одно попадание; б) хотя бы одно попадание в мишень. Ответ: 0,36; 0,91.

7.3.6. Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найдите вероятность того, что охотник: а) промахнется все 3 раза; б) попадет хотя бы один раз; в) попадет два раза. Ответ: 0,024; 0,976; 0,452.

7.3.7. В ящике семь белых и восемь черных шаров. Из ящика вытащили один шар, а затем второй (без возвращения). Какова вероятность, что второй вынутый шар белый? Ответ: 0,467.

7.3.8. В группе десяти студентов, пришедших на экзамен, трое подготовлены отлично, четверо – хорошо, двое – удовлетворительно и один – плохо. Имеется двадцать вопросов, причем: отлично подготовленный студент может ответить на все, хорошо подготовленный – на шестнадцать, удовлетворительно подготовленный – на десять и плохо подготовленный – на пять. Найдите вероятность того, что случайно выбранный студент сможет ответить на доставшийся ему вопрос; и вероятность того, что этот студент плохо подготовлен, и ему просто повезло с вопросом. Ответ: 0,745; 0,034.

7.3.9. Студент выучил тринадцать из пятнадцати вопросов. Что для него выгоднее – отвечать первым или вторым? Ответ: нет разницы.

7.3.10. Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых автомашин, проезжающих по шоссе, как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала машина. Найдите вероятность того, что это грузовая машина. Ответ: 0,43.

7.3.11. Магазин «Автозапчасти» получает ремни генератора от двух поставщиков в отношении 4:5. Ремни от первого поставщика рвутся в течение 50 000 км пробега в каждом десятом случае, а от второго – в каждом двадцатом случае. Найдите вероятность того, что купленный в магазине ремень не порвется в течение 50 000 км пробега. Ответ: 0,93.

7.3.12. Преподаватель к зачету подготовил пятьдесят задач: двадцать по теории вероятностей и тридцать по статистике. Для зачета нужно решить первую доставшуюся наугад задачу. Студент умеет решать восемнадцать задач по теории вероятностей и пятнадцать задач по статистике. а) Какова вероятность для студента сдать зачет? б) Студент сдал зачет. Какова вероятность, что ему досталась задача по теории вероятностей? Ответ: 0,66; 0,54.

7.3.13. Тридцать процентов пациентов, поступивших в больницу, принадлежат к первой социальной группе, двадцать процентов – ко второй, пятьдесят – к третьей. Вероятности заболевания туберкулезом для представителя каждой социальной группы соответственно равны 0,02; 0,03 и 0,01. Проведенные анализы для случайно выбранного пациента показали наличие туберкулеза. Найдите вероятность того, что это представитель третьей группы. Ответ: 0,29.

7.3.14. В сеансе одновременной игры в шахматы с гроссмейстером играют десять перворазрядников, пятнадцать второразрядников. Вероятность того, что в таком сеансе перворазрядник выиграет у гроссмейстера равна 0,2, для второразрядника эта вероятность равна 0,1. Случайно выбранный участник выиграл. Найдите вероятность того, что это был второразрядник. Ответ: 0,43.

7.3.15. Шестьдесят процентов учащихся в школе – девочки. Восемьдесят процентов девочек и семьдесят пять процентов мальчиков имеют билеты в театр. В учительскую принесли кем-то потерянный билет. Какова вероятность того, что этот билет принадлежит девочке? мальчику? Ответ: 0,62; 0,38.

7.3.16. Для участия в студенческих спортивных соревнованиях выделено из первой группы четыре студента, из второй – шесть, из третьей – пять. Вероятности того, что отобранный студент из первой, второй и третьей групп попадет в сборную университета, равны соответственно 0,5; 0,4 и 0,3. Наудачу выбранный студент попал в сборную. К какой из этих групп он вероятнее всего принадлежит? Ответ: ко второй.

7.3.17. В 10 машин грузят ящики с фруктами. Среди них 10 ящиков с фруктами III сорта. Какова вероятность того, что никакие два из них не попадут в одну машину.

7.3.18. В совхозе второй тарифный разряд имеют 5% всех работающих, третий – 30%, четвертый – 20%, пятый – 30%, остальные – высший разряд. Найти вероятность того, что из двух наудачу выбранных рабочих: а) хотя бы один имеет высший разряд; б) оба имеют одинаковый разряд.

7.3.19. При включении зажигания двигатель начнет работать с вероятностью 0,7. Найти вероятность того, что а) двигатель начнет работать со второго раза включения зажигания; б) для запуска двигателя придется включать зажигание не более 3-х раз.

7.3.20. В магазине было продано 200 из 250 кг яблок трех сортов, имевшихся в количествах 50, 70 и 130кг. Какова вероятность того, что остались нераспроданными яблоки одного сорта, если для каждого сорта одна и та же вероятность быть проданным.

7.3.21. Вероятность получения дохода по итогам года для фермера составляет 0,85. Найти вероятность того, что из выбранных наудачу 3-х фермеров: а) только один получит доход; б) по крайней мере один получит доход.

7.3.22. В совхозе три тракторные бригады. Вероятность невыполнения плана первой бригадой составляет 0,02; второй – 0,05; третьей – 0,01. Найти вероятность того, что к моменту подведения итогов плановое задание: а0 будет выполнено всеми бригадами; б) не выполнено ни одной.

7.3.23. Установлено, что 15% банок импортных мясных консервов и 10% отечественных были низкого качества. В продаже импортные и отечественные консервы представлены в количествах, относящихся как 4:6. Найти вероятность того, что наудачу выбранная банка мясных консервов – хорошего качества.

7.3.24. На сборку поступают детали с двух конвейеров. Вероятность поступления бракованной детали с 1-го конвейера – 0,15, со второго – 0,05. На сборку поступило 20 деталей с 1-го конвейера и 30 – со второго. Найти вероятность того, что наудачу взятая деталь окажется бракованной.

7.3.25. Колхоз может получить трактор с одного из трех тракторных заводов. Вероятность того, что этот трактор будет изготовлен на первом заводе, равна 0,3; на втором – 0,2 и на третьем – 0,5. Вероятность изготовления первым заводом трактора отличного качества равна 0,65, вторым – 0,7; третьим – 0,75. Найти вероятность того, что полученный колхозом трактор будет отличного качества.

7.3.26. На склад поставляют томаты три бригады. В продукции первой бригады 90% продукции высшего качества, второго – 85%, третьего – 75%, причем число бракованных томатов относится как 3:5:2. Найти вероятность того, что взятый наудачу томат окажется бракованным.

7.3.27. В магазин продукция поставляется тремя фирмами в соотношении 8:5:7. Среди продукции первой фирмы продукция высшего качества составляет 85%, второй – 90%, третьей – 70%. Приобретенный продукт оказался высшего качества. Какова вероятность того, что он произведен первой фирмой?

7.3.28. На завод поступает продукция трех совхозов. Объемы продукции относятся как 2:3:5. Известно, что средний процент нестандартной продукции в первом совхозе равен 3%, во втором – 2% и в третьем – 1%. Наудачу взятая продукция оказалась стандартной. Каким совхозом она была поставлена?

7.3.29. В совхозе вероятность получения прибыли в урожайный год составляет 0,13 от общего объема реализации, а в неурожайный – только 0,08. Вероятность урожайного года 0,8. Какова вероятность получения прибыли в следующем году?

В прошлом году общий объем реализации составил 20 млн.руб. и год был урожайным. Сколько прибыли получил совхоз в прошлом году?