Свойства произведения матриц
1. 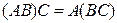 . 2.
. 2. 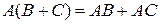 ,
, 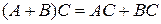 .
.
3. 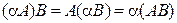 . 4.
. 4. 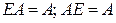 . 5.
. 5. 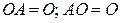 .
.
Все свойства справедливы только в тех случаях, когда произведения матриц в левой (или правой) части равенства существуют. Первое свойство носит название ассоциативности, второе – дистрибутивности умножения относительно сложения.
Пример 10.7. Известно произведение 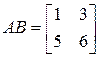 . Найти:
. Найти:
а) 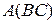 , если
, если 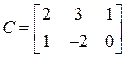 ;
;
б) 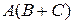 , если
, если 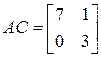 .
.
∆ На основании свойств получаем:
а) 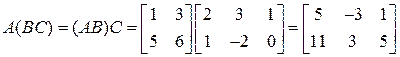 ;
;
б) 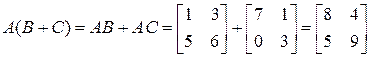 .▲
.▲
Степени квадратной матрицы.Если 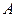 – квадратная матрица, то определено произведение
– квадратная матрица, то определено произведение 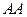 , которое называется квадратом матрицы
, которое называется квадратом матрицы 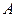 и обозначается
и обозначается 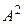 . Квадрат матрицы
. Квадрат матрицы 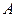 является квадратной матрицей того же порядка, что и
является квадратной матрицей того же порядка, что и 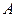 , поэтому определено и произведение
, поэтому определено и произведение 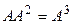 и так далее: для любого натурального числа
и так далее: для любого натурального числа 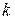 по определению
по определению 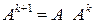 .
.
Квадратная матрица перестановочна с любой своей натуральной степенью, т.е. для любой квадратной матрицы 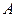 и для любого натурального
и для любого натурального 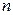 справедливо равенство
справедливо равенство 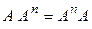 , перестановочны также любые натуральные степени одной и той же квадратной матрицы. Более того, если матрицы
, перестановочны также любые натуральные степени одной и той же квадратной матрицы. Более того, если матрицы 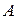 и
и  перестановочны, то перестановочны и любые их натуральные степени.
перестановочны, то перестановочны и любые их натуральные степени.
Если 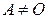 , то по определению считается, что
, то по определению считается, что 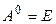 .
.
Пример 10.8. Докажите, что для произвольных перестановочных матриц 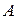 и
и  при любом натуральном
при любом натуральном  справедливо равенство
справедливо равенство
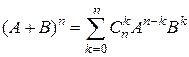 – (10.1)
– (10.1)
формула бинома Ньютона.
∆ Доказательство проведем методом математической индукции.
1. При 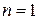 получаем:
получаем: 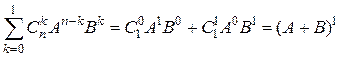 – равенство истинно.
– равенство истинно.
2. Предположим, что равенство верно при 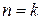 , и докажем его для
, и докажем его для 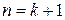 (в квадратных скобках будем пояснять выполняемые действия):
(в квадратных скобках будем пояснять выполняемые действия):
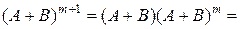 [применяем предположение индукции]
[применяем предположение индукции]
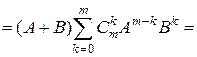 [раскрываем скобки]
[раскрываем скобки]
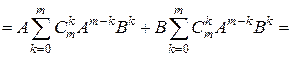 [множители, не зависящие от индекса суммирования, вносим под знак суммы и используем перестановочность матриц
[множители, не зависящие от индекса суммирования, вносим под знак суммы и используем перестановочность матриц 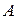 и
и  ]
] 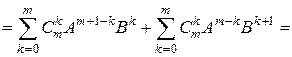
[в первой сумме отделяем первое слагаемое, а во второй – последнее]
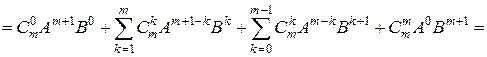
[во второй сумме делаем замену индекса 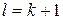 ]
]
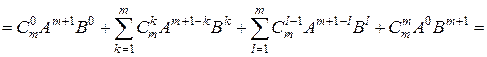
[во второй сумме полагаем 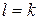 ]
] 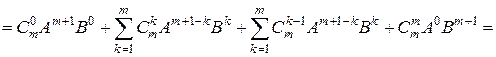
[объединяем две суммы в одну]
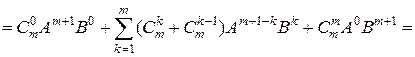 [используем свойства биномиальных коэффициентов
[используем свойства биномиальных коэффициентов 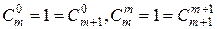 ,
, 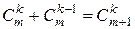 ]
] 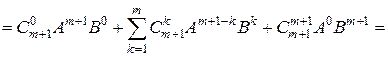
[все слагаемые объединяем в одну сумму] 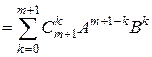 .▲
.▲
Пример 10.9.Найти  -ю степень матрицы
-ю степень матрицы 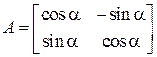 .
.
∆ На основании определения с использованием результата примера 10.4 при 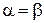 получаем:
получаем:
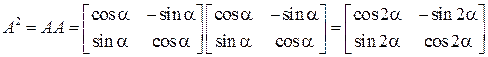
При каждом последующем умножении на матрицу 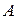 к аргументу просто будет прибавлять еще одно слагаемое
к аргументу просто будет прибавлять еще одно слагаемое  . Окончательно получим
. Окончательно получим 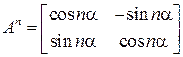 ▲
▲
Пример 10.10.Вычислить  -ю степень для следующих матриц:
-ю степень для следующих матриц:
а) 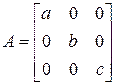 ; б)
; б) 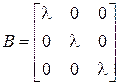 ; в)
; в) 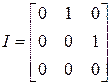 ; в)
; в) 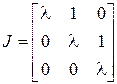 .
.
∆ а) На основании примера 10.5 а) получаем
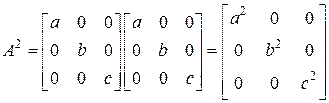 ;
; 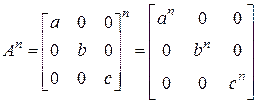 .б) Частный случай примера а):
.б) Частный случай примера а): 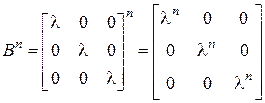 .
.
в) На основании примера 10.5 б) при умножении матрицы  на любую матрицу слева столбцы последней передвигаются на одну позицию вправо. Таким образом,
на любую матрицу слева столбцы последней передвигаются на одну позицию вправо. Таким образом,
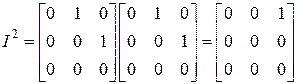 ;
;
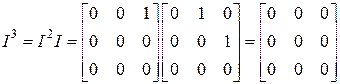 .
.
Так как третья степень матрицы  – нулевая матрица, то и все последующие ее степени также будут нулевыми матрицами.
– нулевая матрица, то и все последующие ее степени также будут нулевыми матрицами.
в) Запишем матрицу 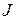 в виде
в виде 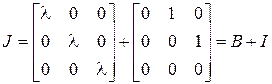 .
.
При решении примера 10.5 доказано, что матрицы  и
и  коммутируют, поэтому можно воспользоваться формулой (10.1):
коммутируют, поэтому можно воспользоваться формулой (10.1): 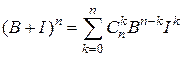 . Так как все степени матрицы
. Так как все степени матрицы  , начиная с третьей, равны нулевой матрице, то в правой части останется только три слагаемых. Таким образом,
, начиная с третьей, равны нулевой матрице, то в правой части останется только три слагаемых. Таким образом,
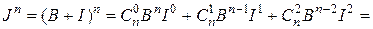
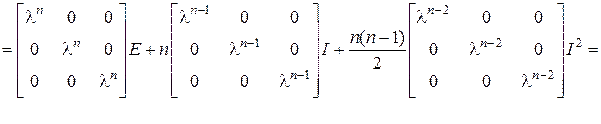
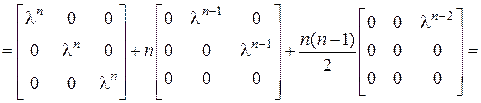
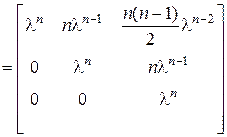 .
.
Замечание. Отметим следующий интересный факт: в каждой строке матрицы 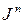 , начиная с диагонального элемента, последовательно записаны слагаемые бинома
, начиная с диагонального элемента, последовательно записаны слагаемые бинома 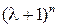 , причем их будет столько, сколько позволяет порядок матрицы. Это утверждение справедливо и для матриц
, причем их будет столько, сколько позволяет порядок матрицы. Это утверждение справедливо и для матриц 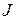 любого порядка. Так, например, если
любого порядка. Так, например, если
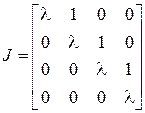 ,
,
то 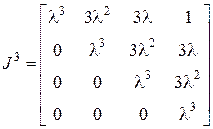 ;
; 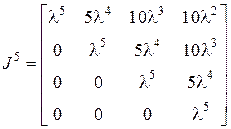 .▲
.▲
Определение 10.4. Пусть задан некоторый многочлен 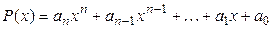 . Для любой квадратной матрицы
. Для любой квадратной матрицы 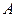 будем считать по определению, что
будем считать по определению, что
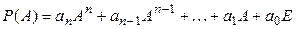 .
.
Если 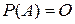 , то говорят, что матрица
, то говорят, что матрица 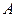 является корнем многочлена
является корнем многочлена 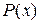 .
.
Пример 10.11.Доказать, что матрица 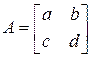 является корнем многочлена
является корнем многочлена 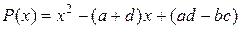 .
.
∆ Согласно определению 10.4 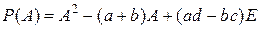 . Найдем вначале
. Найдем вначале 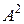 :
: 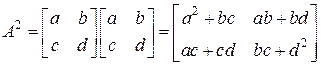 . Тогда
. Тогда
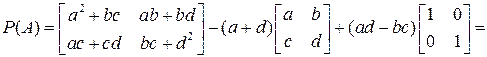
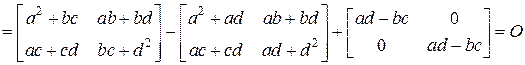 , что и требовалось доказать. ▲
, что и требовалось доказать. ▲
Пример 10.12.Для матрицы 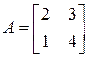 найти
найти 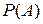 для следующих многочленов:
для следующих многочленов:
а) 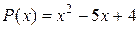 ; б)
; б) 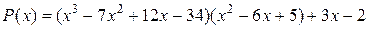 .
.
∆ а) Поступаем так же, как и в предыдущем примере:
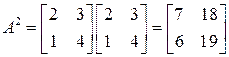 ;
; 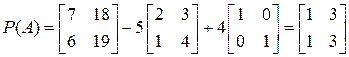 ;
;
б) На основании примера 10.11 получаем 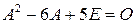 . Поэтому первое слагаемое равно нулевой матрице независимо от того, каким будет первый сомножитель. Значит,
. Поэтому первое слагаемое равно нулевой матрице независимо от того, каким будет первый сомножитель. Значит,
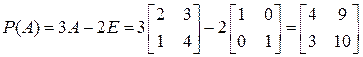 . ▲
. ▲
Транспонирование матриц
Определение 10.5. Матрица 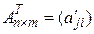 называется транспонированной к матрице
называется транспонированной к матрице 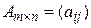 , если
, если
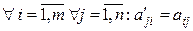 .
.
Другими словами, при транспонировании матрицы строки становятся столбцами и наоборот. Кроме обозначения 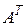 для матрицы, транспонированной к
для матрицы, транспонированной к 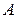 , используют еще и следующие:
, используют еще и следующие: 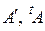 .
.
Свойства операции транспонирования
1. 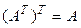 ; 3.
; 3. 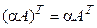 ;
;
2. 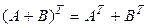 ; 4.
; 4. 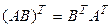 .
.
Пример 10.13. Даны матрицы 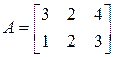 и
и 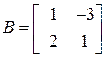 . Из произведений
. Из произведений 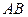 ,
, 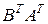 ,
, 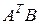 , и
, и 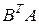 найти те, которые существуют.
найти те, которые существуют.
∆ Матрица 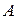 имеет размеры
имеет размеры  ,
, 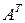 – размеры
– размеры 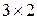 ,
,  и
и 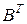 – размеры
– размеры 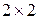 . Определены произведения
. Определены произведения 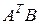 и
и 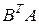 . Приступаем к вычислениям:
. Приступаем к вычислениям:
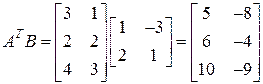 ;
; 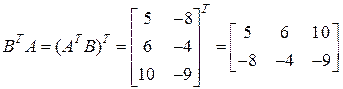 .▲
.▲
