Глава 3. элементы аналитической геометрии 2 страница

Пусть даны две плоскости

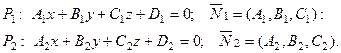
Угол между плоскостями равен углу между их нормаль –

ными векторами :

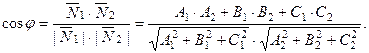(6)

Условие параллельности плоскостей:

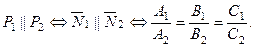(7)

Условие перпендикулярности плоскостей:

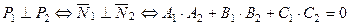. (8)

Если , то уравнения задают одну и ту же плоскомть.

Пример 4. Найти угол между плоскостям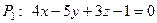и и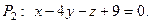

. Тогда, по формуле (6),

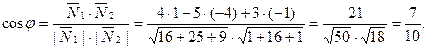
§ 4. ПРЯМАЯ В ПРОСТРАНСТВЕ

Любую прямую в пространстве можно задать пересечением двух не параллельных плоскостей, т.е. система двух уравне -ний плоскостей представляет собой общиеуравнения прямой, которая получается при их пересечении:

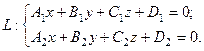(1)

Здесь и - не

коллинеарные нормальнве векторы данных плоскостей, т.е. их координаты не пропорциональны.

Иначе уравнение прямой можно задать следующим образом:

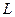
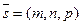
- фиксированная точка данной прямой, - текущая точка прямой, 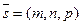- направляя- ющий вектор прямой. Тогда уравнение прямой получается из условия коллинеарности (т.е. пропорциональности) векторов и , т.е. по формуле:

(2)

Уравнения (2) называются каноническими уравнениями прямой.

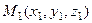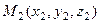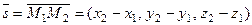В частности, если на прямой заданы две точки и , то в качестве направляющего вектора можем взять вектор и уравнение прямой в этом случае принимает вид:

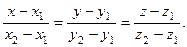(3)

Например: Написать уравнение прямой, проходящей через точки .

По формуле (3), получаем:

.

Если в равенстве (2) введём параметр

,

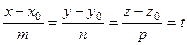то получим параметрическое уравнение данной прямой:

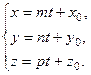(4)

Переход от общих уравнений к каноническим выполняется следующим образом: из рисунка

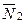
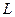
видим, что направляющий вектор прямой 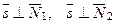(как вектор, лежащий в соответствующих плоскостях) можно найти через векторное произведение векторов, т.е., если прямая задана общими уравнениями:

(5) и , , то

.

Но для того, чтобы написать каноническое уравнение пря -мой, необходимо знать какую – нибудь точку на данной пря -мой. Чтобы найти какую – нибудь точку, в системе (5) зафиксируем одну координату, например, положим 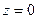, а остальные две найдём как решение системы.

Рассмотрим пример:

Написать канонические уравнения прямой:

В данном случае, 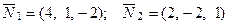. Тогда

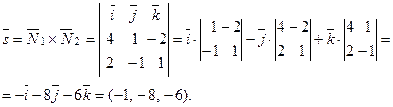
Теперь найдём какую – нибудь точку на этой прямой. В данном примере удобно положить 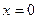. Получаем систему:

Сложим эти уравнения: тогда 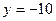и точка лежит на прямой, следовательно, её кано- нические уравнения можно записать в виде:

Угол между прямыми в пространстве равен углу между их направляющими векторами, т.е. для прямых 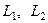с направ– ляющими векторами :

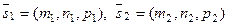Если прямые параллельны, то и получаем условие параллельности прямых: .

Если прямые перпендикулярны, то 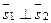и из условия ортогональности векторов получаем условие перпендикуляр -ности прямых:

Пример. Доказать перпендикулярность прямых:

и

Направляющий вектор первой прямой: 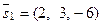; на –правляющий вектор второй прямой: , где

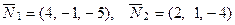. Тогда

т.е. . Проверим условие перпендикулярности плос- костей: 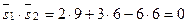. Направляющие векторы ортогональны, следовательно, прямые перпендикулярны.

§ 5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И

ПЛОСКОСТИ В ПРОСТРАНСТВЕ

Прямая и плоскость в пространстве могут быть либо парал- лельными, либо пересекаться.

Пусть заданы уравнения плоскости 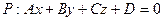и прямой 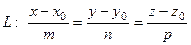. Нормальный вектор плоскости 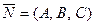, направляющий вектор прямой: . Если прямая параллельна плоскости, то её на- правляющий вектор ортогонален нормальному вектору плос - кости:

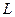
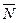
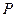
т.е. и, из условия ортогональности векторов:

. (1)

Если прямая перпендикулярна плоскости, то нормальный вектор плоскости коллинеарен направляющему вектору прямой:

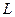
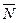
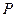
Тогда условие перпендикулярности прямой и плоскости: 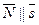, или . (2)

Угол между прямой и плоскостью можно определить следу- ющим образом:

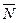
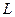
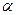
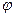
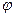
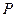
Из чертежа видно, что .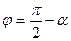

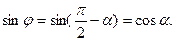
Но 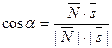. Тогда

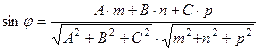(3) 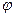- угол между прямой и плоскостью в пространстве.

Рассмотрим примеры:

1. Найти угол между плоскостью, проходящей через точки:

и прямой

.

Нормальный вектор плоскости 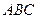ищется, как векторное произведение векторов:

Направляющий вектор прямой 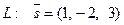. Тогда, по формуле (3),

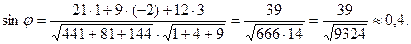
Тогда .

2. При каком значении 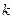прямая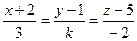

параллельна плоскости ?

Направляющий вектор прямой , нормальный вектор плоскости . Тогда, по условию (1), пря- мая параллельна плоскости, если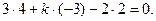

Тогда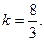

Следующая задача, связанная с взаимным расположением прямой и плоскости в пространстве - это задача: найти точку пересечения прямой и плоскости

Чтобы решить эту задачу, следует записать уравнение пря- тмой 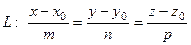в параметрической форме, т.е.

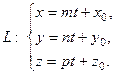
и, подставив значения переменных в уравнение плоскости 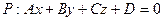, найти значение параметра в точке пересечения. После этого можно найти значения координат точки пересечения.

Пример 3. Найти точку пересечения плоскости

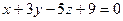и прямой .

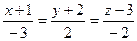Запишем параметрические уравнения прямой:

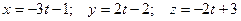(4)

и подставим данные значения в уравнения плоскости. Получим

Тогда точка пересечения имеет координаты:

т.е.

Расстояние от точки до прямой. Чтобы найти расстояние от точки до прямой 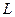, следует написать уравнение плоскости, проходящей через заданную точку перпендикулярно данной прямой; найти точку пересечения полученной плоскости и данной прямой; и после этого найти расстояние от этой точки пересечения до точки .

Пример 4. Найти расстояние от точки 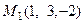до прямой .

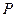
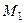
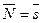
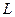
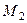
Нормальный вектор плоскости, перпендикулярной прямой 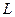, совпадает с направляющим вектором прямой, т.е.

,

Тогда уравнение плоскости имеет вид:

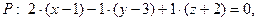или .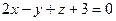

Чтобы найти точку пересечения прямой 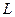и плоскости напишем пераметрическое уравнение прямой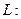

.

Подставив значения неизвестных в уравнение плоскости 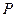, найдём значение параметра в точке пересечения:

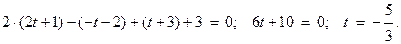
Тогда точка 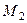имеет координаты:

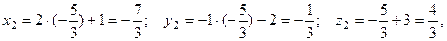т.е. .

Расстояние от точки до прямой 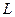найдём как длину отрезка .

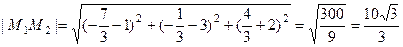Для определения расстояния от точки 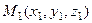до прямой 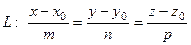можно выбрать и другой способ. Рассмотрим рисунок:

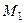
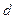
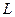
Площадь этого параллелограмма равна , или . Приравняв эти выражения, получим формулу для расстояния от точки до прямой:

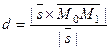. (5)

Решим пример (4) этим способом:

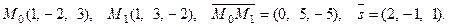
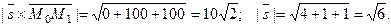
Тогда, по формуле (5),

Вторым способом получили тот же результат.

Следующие две задачи: написать уравнение плоскости, проходящей через две параллельные прямые и плоскости, проходящей через две пересекающиеся прямые, рассмотрим на примерах.

Пример 5. Проверить параллельность прямых и написать уравнение плоскости, проходящей через эти прямые:

Направляющий вектор первой прямой: 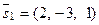; на- правляющий вектор второй прямой - . Эти векторы коллинеарны, так как их координаты пропорциональ- ны, следовательно 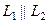. Через две параллельные прямые можно провести единственную плоскость.

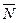
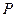
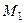
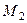
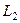
Координаты точек 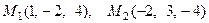получаем из уравнений соответствующих прямых. Нормальный вектор плоскости равен 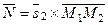, где .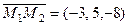

Тогда

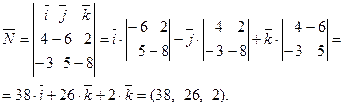
В качестве фиксированной точки плоскости можем взять, например, точку 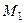, лежащую на первой прямой. В резуль -тате получаем следующее уравнение плоскости:

,

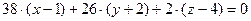Или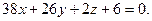

Пример 6. Проверить, что прямые пересекаются и напи -сать уравнение плоскости, проходящей через эти прямые:

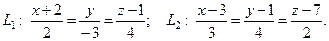
Для данных прямых

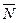
P

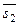
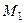
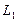
Точки лежащие на этих прямых:

,

тогда .

Если прямые лежат в одной плоскости, то векторы 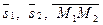компланарны, и их смешанное произведение равно нулю, т.е. .

В нашем случае,

Следовательно, прямые лежат в одной плоскости. Нормаль -ный вектор этой плоскости:

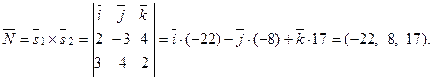Тогда уравнение плоскости имеет вид:

,

или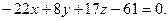

Расстояние между скрещивающимися прямыми:

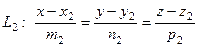, с направляющими векторами 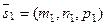, , 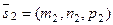проходящими через точк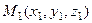и и 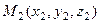можно найти как высоту параллелепипеда, построенного на векторах .

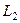
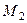
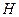
Объём этого параллелепипеда равен: 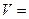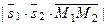. С другой стороны этот же объём равен: .

Тогда

(6)