Методы построения эффективных алгоритмов

Метод „Разделяй и властвуй"

Одним из самых важных и наиболее широко применимых методов проектирования эффективных алгоритмов является метод, называемый методом декомпозиции (или метод "разделяй и властвуй", или метод разбиения). Этот метод предполагает такую декомпозицию (разбиение) задачи размера п на более мелкие задачи, что на основе решений этих более мелких задач можно легко получить решение исходной задачи.

Мы уже познакомились с примерами задач, которые допускают решение таким способом:

Одной из таких задач является сортировка слиянием

Любой алгоритм, решающий задачу методом «Разделяй и властвуй» состоит из нескольких шагов:

1. Разбиение задачи на несколько подзадач меньшей размерности, которые имеют такую же структуру, а следовательно каждая из них разрешима методом «Разделяй и властвуй»
2. Преобразование решений подзадач в одно решение

Такая схема фактически предлагает рекурсивный алгоритм решения, и необходим некоторый механизм выхода из циклов, возникающих при этом. Поскольку размерность подзадач с увеличением глубины рекурсии уменьшается, то через определенное число шагов можно получить можно получить задачи, имеющие константную размерность, каждая из которых решается каким либо способом за константное время. Тогда можно построить рекуррентные соотношения для времени выполнения программы:

Здесь ,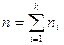

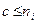
В качестве примера рассмотрим алгоритм умножения двух 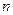разрядных двоичных чисел. Традиционный метод «умножение столбиком требует 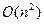операций.

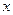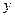Пусть и два 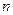разрядных двоичных числа. Без ограничения общности положим, что 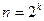. Разобъем 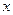и 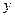на две части: старшую и младшую:

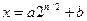и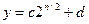

Тогда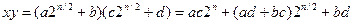

В таком виде, умножение 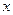на 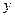реализуется с помощью 4-х умножений n/2 разрядных чисел, нескольких сдвигов и сложений. Применение алгоритма в таком виде не дает преимуществ по сравнению с обычным умножением. Сдругой стороны понятно, что операции умножения и сложения имеют различные веса. Рассмотрим модификацию алгоритма, позволяющую несколько уменьшить число умножений.

В самом деле положим:

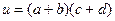
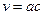
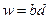
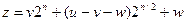
Такой подход требует всего трех умножений и нескольких сложений и сдвигов. Сложения и сдвиги занимают 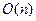времени.

Поэтому,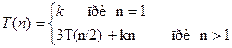

Решением такой системы будет 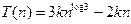. Доказательство проводится индукцией по .

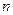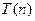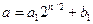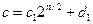Для завершения доказательства необходимо упомянуть, что произведение вообще то является произведением двух (n/2+1) разрядных чисел, что нарушает рекурсивное соотношение для . Запишем и , где 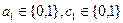. Тогда 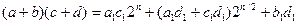. Слагаемое 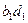вычисляется с помощью нашего алгоритма, остальные произведения требуют 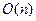операций, поскольку являются операциями над битами.

Вначале кажется, что уменьшение числа ( 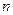/2)-разрядных произведений с четырех до трех может уменьшить общее время в лучшем случае на 25%. Однако соотношения применяются рекурсивно для вычисления ( 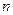/2)-разрядных, ( 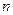/4)-разрядных и т. д. произведений. Эти 25-процентные уменьшения объединяются и дают в результате асимптотическое улучшение временной сложности.

Временная сложность процедуры определяется числом и размером подзадач и в меньшей степени работой, необходимой для разбиения данной задачи на подзадачи. Так как рекуррентные уравнения часто возникают при анализе рекурсивных алгоритмов типа „разделяй и властвуй", рассмотрим решение таких уравнений в общем виде.

Теорема 2.1. Пусть а, 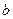и с— неотрицательные постоянные.

Решение рекуррентных уравнений

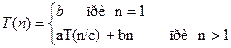
где 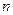— степень числа с, имеет вид,

Доказательство. Если 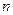— степень числа 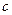, то

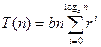, где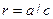

Если a 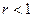, то ряд сходится и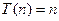

Если а=с, то каждым членом этого ряда будет 1, а всего в нем О (log n) членов. Поэтому 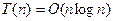. Наконец, если а>с, то сумма ряда равна =

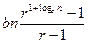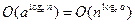
Из теоремы 2.1 вытекает, что разбиение задачи размера 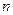(за линейное время) на две подзадачи размера 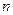/2 дает алгоритм сложности 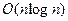. Если бы подзадач было 3, 4 или 8, то получился бы алгоритм сложности порядка 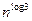, , 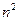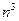соответственно.

С другой стороны, разбиение задачи на 4 подзадачи размера 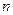/4 дает алгоритм сложности 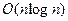, а на 9 и 16 — порядка 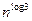и 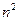соответственно. Поэтому асимптотически более быстрый алгоритм умножения целых чисел можно было бы получить, если бы удалось так разбить исходные целые числа на 4 части, чтобы суметь выразить исходное умножение через 8 или менее меньших умножений. Другой тип рекуррентных соотношений возникает в случае, когда работа по разбиению задачи не пропорциональна ее размеру. Если 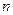не является степенью числа с, то обычно можно вложить задачу размера 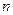в задачу размера 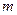, где 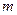— наименьшая степень числа с, большая или равная 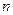. Поэтому порядки роста, указанные в теореме 2.1, сохраняются для любого 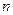. На практике часто можно разработать рекурсивные алгоритмы, разбивающие задачи произвольного размера на с равных частей, где с велико, насколько возможно. Эти алгоритмы, как правило, эффективнее (на постоянный множитель) тех, которые получаются путем представления размера входа в виде ближайшей сверху степени числа с.