Двумерные случайные величины,функцияраспределения,плотностьраспределения,маргинальныеплотности,формулы для вычисления вероятностноймеры двумерной области,числовые характеристики.

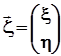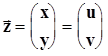Функции распределения и плотности распределенияБудем рассматривать двумерный случайный вектор .будем считать, что случайный вектор принимает значения .Функция распределения двумерного случайного вектора есть вероятность совместного осуществления событий: 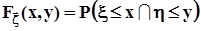Плотность распределения, как и ранее, есть производная от функции распределения по обоим аргументам:

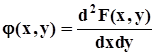,поэтому .

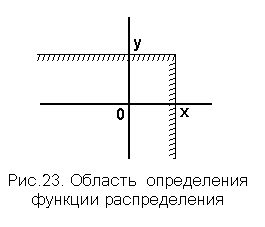
В силу монотонности вероятностной меры функция распределения - неубывающая функция по каждому аргументу, а потому плотность распределения есть неотрицательная функция двух аргументов, которая описывает некоторую поверхность над координатной плоскостью. Эта поверхность приближается к плоскости XOY при удалении значений аргументов от начала координат по любому направлению. Понятно, что 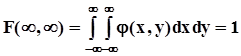.Если по одному из аргументов ограничений нет, то 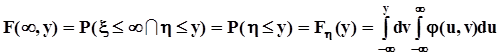. Таким образом мы получили маргинальные (частные) функции распределения 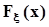и 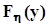. Дифференцирование этих функций по их аргументам, то есть дифференцирование соответствующих интегралов по их верхним пределам, по определению, дает маргинальные (частные) плотности распределения: , .

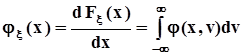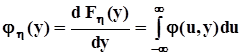Числовые характеристики

Моменты случайных величин определяются, как и ранее, формулами

- начальные моменты k - го порядка 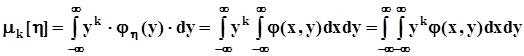.- центральные моменты k - го порядка:

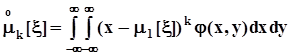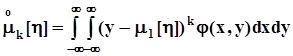, .Среди этих моментов самыми употребительными являются математи­ческие ожидания и дисперсии , . Математическое ожидание случайного вектора есть вектор, компонентами которого являются математические ожидания соответствующих составляющих:

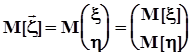.Из условных моментов выделим лишь первые начальные (условные математические ожидания) и вторые центральные (условные дисперсии): , , , 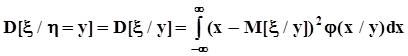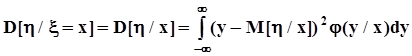.Как и ранее, во всех случаях 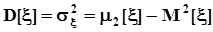, , , 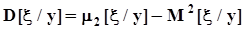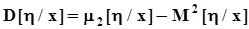.Для двумерных случайных величин вводятся смешанные моменты:- начальные порядка k, r ,

-центральные порядка k, r :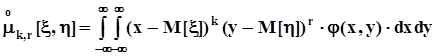 .Из них наиболее употребительным является центральный смешанный момент порядка (1, 1),который называется ковариацией и обозначается, как cov(x, h): .Выясним связь между этим и начальным смешанным моментом того же порядка.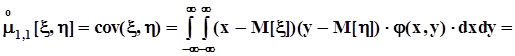

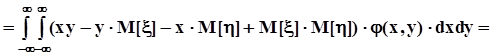
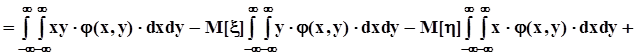
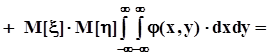
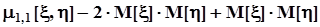.В итоге получаем, что 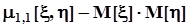Если случайные величины x и hнезависимы,в соответствии с признаком независимости, сформулированным выше,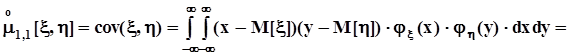= ,то есть мы видим, что двукратный интеграл в этих условиях преобразуется в произведение однократных интегралов, каждый из которых равен нулю. В самом деле, 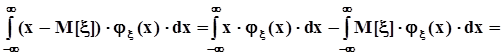.Поэтому при условии независимости случайных величин x и hих первый центральный смешаный момент или ковариация равна 0.В случае взаимнооднозначной зависимости междуx и h,например, линейной ковариация равна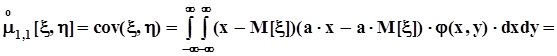 .
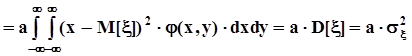