Корреляция в рядах динамики

Корреляция между уровнями временных рядов может иметь место и при отсутствии реальной связи между явлениями, т.е. может быть ложная корреляция. Т.к. если ряды динамики характеризуются одинаковой тенденцией, то им всегда будет присуща высокая корреляция. Если ряды динамики хар-ся наличием тренда, то при изучении корреляции и построении ур-я регрессии необходимо исключить тренд.

Если рядам динамики присущи также периодические колебания, то при изучении корреляции из первоначальных данных следует исключить обе компоненты: тренд и сезонные колебания.

В зависимости от того, какая выдвигается гипотеза о форме связи остаточных величин (лин. или нелин.), используются разные показатели корреляции.

При линейной связи: между остаточными величинами рядов (e_y и e_x) теснота измеряется линейным коэф-ом корреляции:

r_exey =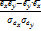

Т.к. Σ e_x = Σ e_y = 0, то формула упрощается:

r_exey =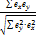

При нелинейной связи остаточных величин оценка тесноты связи дается с помощью индекса корреляции:

R_exey = .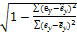

Где:

е_у – остаточные величины ряда у, например отклонение от тренда e_y=y_t-ŷ_t;

ě_у – теор. значения остатков, рассчитанные на основе ур-я регрессии;

ē_у – средняя величина остатка.

Рассмотренные показатели корреляции находятся в границах: -1≤ r_exey≤1 и 0≤ R_exey≤1, т.е. чем ближе по абс. величине они к 1, тем теснее связь остат. величин.

При наличии в рядах динамики лин. тенденций коэф-т корреляции можно найти, используя цепные абс. приросты, т.е. первые разности (Δх=х_t-x_t-1 и Δy=y_t-y_t-1) по формуле обычного линейного коэф-та корреляции:

r_ΔxΔy = .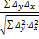

54. Определение модели авторегрессии и модели с распределенными лагами.

В эконометрике к числу динамических относятся не все модели, построенные по временным рядам данных. Термин «динамический» в данном случае характеризует каждый момент времени t в отдельности, а не весь период, для которого строится модель.

Эконометрическая модель является динамической, если в данный момент времени t она учитывает значения входящих в нее переменных, относящиеся как к текущему , так и к предыдущим моментам времени, т.е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.

•

Можно выделить два основных типа динамических эконометрических моделей.

К моделям первого типа относятся модели авторегрессии и модели с распределенным лагом, в которых значения переменной за прошлые периоды времени (лаговые переменные) непосредственно включены в модель.

Модели второго типа учитывают динамическую информацию в неявном виде. В эти модели включены переменные, характеризующие ожидаемый или желаемый уровень результата, иди одного из факторов в момент времени t. Этот уровень считается неизвестным и определяется экономическими единицами с учетом информации, которой они располагают в момент (t - 1).

В зависимости от способа определения ожидаемых значений показателей различают модели неполной корректировки, адаптивных и рациональных ожиданий. Оценка параметров этих моделей сводится к оценке параметров моделей авторегрессии.

При исследовании эк.процессов нередко приходится моделировать ситуации, когда значение результативного признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени t-1, t-2,…,t-l. Величину l характеризует запаздывание в воздействии фактора на результат, в эконометрике называется лагом, а временные ряды самих факторных переменных, сдвинутые на 1 или более моментов, - лаговыми переменными.

Разработка эк.политики как на макро-, так и на микроуровне требует решения обратного типа задач, т.е. задач, определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения эк.показателей (t+1).

Эк.моделирование процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называютя моделями с распределенным лагом.

Модель вида 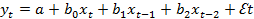является примером модели с распределенным лагом.

Наряду с лаговыми значениями независимых или факторных переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии.

Модель вида 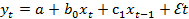является примером модели авторегрессии.

Построение модели с распределенным лагом и моделей авторегрессии имеет свою специфику:

1. оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть проведена с помощью обычного МНК, а требует специальных статистических методов

2. исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры

3. между моделями с распределенным лагом и моделями авторегрессии имеется определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому