Непрерывные случайные величины

Определение 1.Случайная величина ξ называется непрерывной случайной величиной (обозначение НСВ), если её функция распределения F(x) непрерывна при всех значениях x.

Принимая во внимание формулу (4) из §1 получаем, что для НСВ вероятность каждого её отдельного значения равна нулю.

Значение НСВ уже могут заполнять конечный или бесконечный промежуток (α,β) числовой оси.

Один из способов построения НСВ заключается в следующем. Рассмотрим неотрицательную интегрируемую функцию P(x), определённую на всей числовой оси и удовлетворяющую условию:

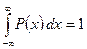. (1)

Положим

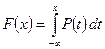. (2)

Определённая таким образом функция F(x) обладает всеми характеристическими свойствами функции распределения (см.§1), к тому же она будет непрерывной. Значит (см.теорема 3.§1) функция F(x) является функцией распределения некоторой случайной величины ξ.

Чаще всего рассматривают НСВ, обладающие плотностью.

Определение 2. Мы будим говорить, что случайная величина ξ распределена с некоторой плотностью, если существует неотрицательная функция P_ξ(x), Такая, что для всех х справедливо равенство

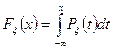, (3)

где F_ξ(x) – функция распределения случайной величины ξ.

Функция P_ξ(x) называется плотностью распределения или плотностью вероятности случайной величины ξ.

В виду выше сказанного ясно, что случайная величина, имеющая плотность вероятности, непрерывна.

Обратное верно не всегда: существуют НСВ, для которых не существует плотности.

Ясно так же, что плотность вероятности должна удовлетворять условию (1), т.е.

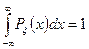. (4)

Это следует из соотношения .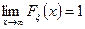

Из определения плотности распределения следует:

1. 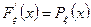в точках непрерывности ,

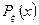2.

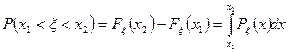
для любых .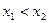

Поясним смысл названия «плотность вероятности».

Согласно выше сказанному

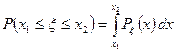. (5)

По теореме о среднем интеграл, стоящей в правой части (5) равен 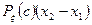, где 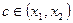, и значит

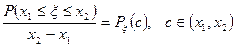. (6)

Левая часть формулы (6) представляет собой среднюю вероятность попадания значений случайной величины ξ на отрезке .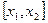

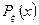Теперь если мы будем стягивать отрезок к некоторой точке и предположим, что непрерывна в этой точке, то мы получим:

.

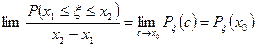Поскольку отношение, стоящее под знаком предела, есть своего рода «вероятность на единицу длины отрезка 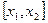», то предел этого отношения 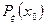естественно рассматривать как плотность вероятности в самой точке 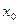_. Значит во всякой точк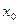е , где 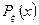непрерывна, число 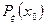совпадает с естественно понимаемой плотностью вероятности в точке 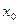. Отсюда и название для функции 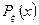- «плотность вероятности».

Непрерывные функции распределения, не имеющие плотностей, называются сингулярными.

Примеры непрерывных случайных величин:

1. Равномерное распределение на отрезке.

Случайная величина ξ имеет равномерное распределение на отрезке 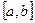, если её плотность вероятности имеет вид

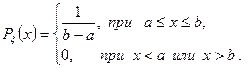(7)

Если какой-либо отрезок 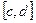содержится в 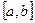, то вероятность попадания в него случайной величины ξ равна:

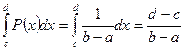. (8)

Таким образом, вероятность попадания в любую часть отрезка 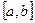пропорциональна длине этой части.

Записав формулу (8) в виде

,

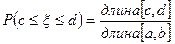мы получим формулу геометрических вероятностей.

Следовательно, можно сказать, что геометрические вероятности порождаются равномерным распределением.

С равномерным распределением мы сталкивается всякий раз, когда по условиям опыта величина ξ принимает значение в конечном промежутке 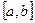, причём все значения из 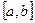возможны в одинаковой степени (ни одно из них не имеет преимуществ перед другими). Например:

а) ξ – время ожидания на стоянке автобуса (величина ξ распределена равномерно на отрезке 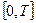, где Т – интервал движения между автобусами.

б) ξ – ошибка при взвешивании случайно выбранного предмета, получающаяся от округления результата взвешивания до ближайшего целого числа (величина ξ имеет равномерное распределение на отрезке 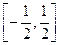, где за единицу принята цена деления шкалы).

Найдём функцию распределения равномерно распределенной случайной величины.

Связь между функцией распределения и плотностью вероятности даётся формулой (3)

.

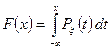Подставляя сюда функцию 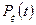из (7) получим:

для , ,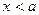

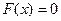для , ,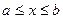

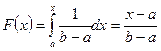для .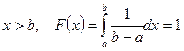

График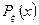и и 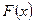показаны на рисунке 1.

Рис. 1