В системе с астатизмом первого порядка
Пример 5.2. Синтезировать регулятор положения с применением ЛЧХ на основе критерия динамической точности системы. Параметры для расчётов принять из примера 5.1. Моментную составляющую ошибки определить при отработке линейно возрастающего момента сопротивления 
.
Решение.Определяем параметры желаемой передаточной функции ЭП (5.8).
Коэффициент передачи по скорости
с– 1.
Коэффициент передачи по ускорению
с– 2.
Значение базовой частоты будет равно
с– 1.
По выражениям (5.8) рассчитываем постоянные времени
с;
с.
Рассчитываем протяжённость среднечастотного участка желаемой ЛАЧХ
.
Частоту, соответствующую максимальному запасу по фазе определяем по формуле
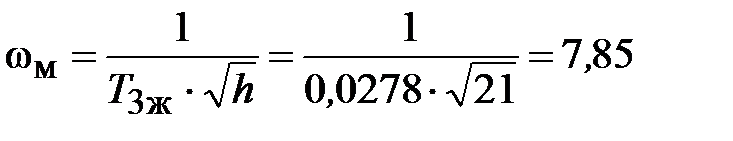с– 1.
По условию обеспечения максимального запаса по фазе находим постоянную времени 
>> 1/ 
= 1/7,85 = 0,127 с.
Принимаем = 2 с.
С учётом проведённых расчётов желаемая передаточная функция ЭП с астатизмом первого порядка запишется как
Составляем программу для определения передаточной функции регулятора положения ЭП с астатизмом первого порядка. Передаточную функцию неизменяемой части принимаем по примеру 5.1.
num1=[128.84 220.617];
den1=[0.0556 2.0278 1 0];
sys1=tf(num1, den1);
num2=[0.005409 0.8371 36.97 397.5];
den2=[4.259e-10 4.09e-07 0.0001152 0.01153 0.5681 14.25 122.2 0];
sys2=tf(num2, den2);
sys3=sys1/sys2
sys3 =
5.487e-08 s^8 + 5.279e-05 s^7 + 0.01493 s^6 + 1.511 s^5 + 75.74 s^4 + 1961 s^3 + 1.889e04 s^2 + 2.696e04 s
-------------------------------------------------------------------------------------------------- 0.0003007 s^6 + 0.05751 s^5 + 3.758 s^4 + 97.91 s^3 + 843 s^2 + 397.5 s
Составляем программу для определения ЛАЧХ регулятора положения, изображенную на рис. 5.9:
num=[5.487e-08 5.279e-05 0.01493 1.511 75.74 1961 1.889e04 2.696e04 0];
den=[0.0003007 0.05751 3.758 97.91 843 397.5 0];
bode(num, den)
Переходим к анализу полученных графиков. Низкочастотный участок ЛАЧХ РП проходит параллельно оси частот, постепенно изменяя наклон к среднечастотному участку в пределах от 0 до –20 дБ/дек и далее к 0 дБ/дек. Высокочастотный участок ЛАЧХ с увеличением частоты изменяет свой наклон также в пределах от 20 до 40 дБ/дек. Полученные ЛАЧХ следует аппроксимировать пятью асимптотами и придать регулятору положения свойства интегро-дифференцирующего регулятора.
Рис. 5.9. ЛАЧХ регулятора положения
Рассчитаем параметры передаточной функции.
Находим коэффициент передачи Крп. Из графика рис. 5.9 имеем
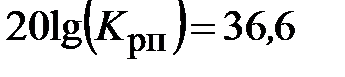дБ,
откуда 
= 67,608. Частоты сопряжения w1 = 0,344 с– 1; w2 = 1,65 с– 1; w3 = 100 с– 1; w4 = 1000 с– 1 и постоянные времени
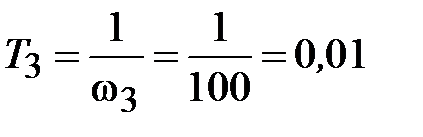с; 
с;
с; 
с.
С учётом полученных значений передаточная функция синтезированного регулятора положения принимает вид
.
Переходим к построению и моделированию ССДМ ЭП, показанной на рис. 5.10. Для формирования линейно возрастающих воздействий 
и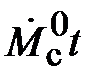 
используются блоки Ramp и Ramp1.
| Рис. 5.10. Структурная схема динамической модели электропривода в среде MatLab |
Результаты моделирования показаны на рис. 5.11 – 5.13.
α(t), рад
t, c
Рис. 5.11. Переходная характеристика системы по задающему воздействию
, рад
t, c
Рис. 5.12. График ошибки системы при линейно возрастающем
задающем воздействии
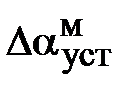, рад
t, c
Рис. 5.13. График моментной составляющей ошибки системы при линейно возрастающем моменте сопротивления
Анализ графика (рис. 5.11) показывает, что следящий позиционный ЭП отрабатывает ступенчатое воздействие 
примерно за 1 с, с перерегулированием 
и числом колебаний N = 2, что соответствует заданному показателю колебательности.
Поскольку система включает интегрирующее звено на выходе, то очевидно, что статическая ошибка будет равна нулю. На рис. 5.12 представлена характеристика ЭП при линейно возрастающем задающем воздействии. В данном случае ошибка по скорости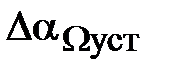 
составляет 17,8 мин.
На рис. 5.13 показан график ошибки, полученный при линейно возрастающем моменте сопротивления Мс. Из графика следует, что влияние возмущающего воздействия сказывается на динамической точности ЭП, а моментная составляющая ошибки 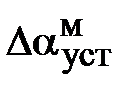составляет 0,58 мин по истечении 4 с. При ступенчатом возмущающем воздействии моментная составляющая установившейся ошибки 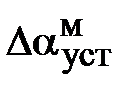будет равна нулю.
Отчётные материалы
1. ЛАЧХ ПИД-регулятора положения.
2. ЛАЧХ интегро-дифферецирующего регулятора положения.
3. ССДМ следящего позиционного электропривода с ПИД-регулятором положения.
4. ССДМ следящего позиционного электропривода с интегро-дифференцирующим регулятором положения.
5. Графики переходных характеристик и ошибок при отработке управляющих и возмущающих воздействий. Анализ графиков.
Контрольные вопросы
1. Пояснить назначение запретной области.
2. Перечислить этапы синтеза регуляторов положения различной конфигурации.
3. Составить алгоритм в среде MatLab для синтеза ПИД-регулятора положения.
4. Составить алгоритм в среде MatLab для синтеза интегро-дифференцирующего регулятора положения.
5. Пояснить порядок аппроксимации ЛАЧХ ПИД-регулятора положения.
6. Пояснить порядок аппроксимации ЛАЧХ интегро-дифференцирующего регулятора положения.
7. Дать сравнительную характеристику передаточных функций интегро-дифференцирующего регулятора и ПИД-регулятора.
8. Пояснить порядок исследования следящего позиционного электропривода с ПИД-регулятором положения.
9. Пояснить порядок исследования следящего позиционного электропривода с интегро-дифференцирующим регулятором положения.
ЛАБОРАТОРНАЯ РАБОТА № 6
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
РЕГУЛЯТОРА ПОЛОЖЕНИЯ