Ауыстырудың жұптығы
Ауыстыру транспозиияның көбейтіндісіне әр түрлі әдіспен жіктелінуі мүмкін. Мысалы,

Алайда, бір ауыстырудың кез келген жіктеуіндегі транспозиция саны төмендегі маңызды қасиетке ие болады.
Лемма (транспозиция саны жайлы). Транспозиция санының жұптығы ауыстырудың транспозицияның көбейтіндісі түрінде берілу әдісіне тәуелді емес.
Дәлелдеуі. Берілген
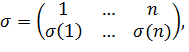
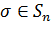
ауыстыруы үшін  жұбын инверсия деп атаймыз, егер
жұбын инверсия деп атаймыз, егер 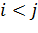 болса, бірақ
болса, бірақ 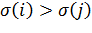 болатын болса. Айталық
болатын болса. Айталық 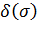 –
– 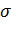 үшін инверсияның жалпы саны болсын. Кез келген τ транспозициясы үшін
үшін инверсияның жалпы саны болсын. Кез келген τ транспозициясы үшін 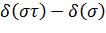 айырымы тақ сан болатындығын дәлелдейік. Айталық
айырымы тақ сан болатындығын дәлелдейік. Айталық 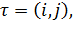
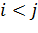 болсын. Онда
болсын. Онда
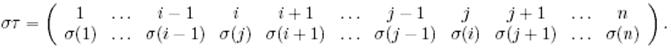
σ ауыстырымы
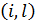 , мұндағы
, мұндағы 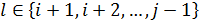 (*)
(*)
түріндегі жұптардың арасында 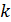 инверсия, ал
инверсия, ал
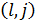 , мұндағы
, мұндағы 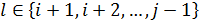 (**)
(**)
түріндегі жұптардың арасында 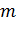 инверсия, және кез келген басқа жұптар арасында
инверсия, және кез келген басқа жұптар арасында 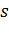 инверсия болсын деп ұйғарайық. Онда
инверсия болсын деп ұйғарайық. Онда 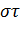 (*) түріндеегі жұптардың арасында
(*) түріндеегі жұптардың арасында 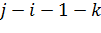 инверсия және (**) түріндегі жұптар арасында
инверсия және (**) түріндегі жұптар арасында 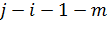 инверсияға ие болады. Сонымен қатар, кез келген басқа жұптар арасында
инверсияға ие болады. Сонымен қатар, кез келген басқа жұптар арасында 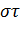 ауыстыруы
ауыстыруы 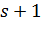 инверсияға ие болады, егер
инверсияға ие болады, егер 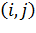 жұбы инверсия болмаса, және керісінше жағдайда
жұбы инверсия болмаса, және керісінше жағдайда 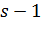 болады. Осылайша,
болады. Осылайша,
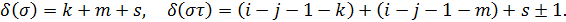
Бұдан
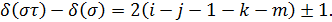
Салдар. Ауыстыруды жіктегенде транспозиция санының жұптығы оның инверсия санының жұптығына сәйкес келеді.
Анықтама. Ауыстыру жұп деп аталады, егер ол жұп транспозиция санының көбейтіндісі болса, кері жағдайда тақ болады.
Сызықтық тәуелділік индикаторының жалғыздығы
 функциясының сызықтық тәуелділік индикаторын құруға қайта оралайық, мұндағы
функциясының сызықтық тәуелділік индикаторын құруға қайта оралайық, мұндағы

векторлары (А), (В), (С) шарттарын қанағаттандырады.
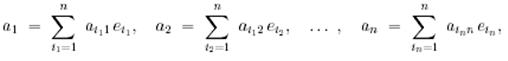
болатындығын көруге болады, мұндағы 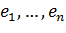 -
- 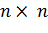 өлшемді бірлік матрицаның бағаны.
өлшемді бірлік матрицаның бағаны.
Егер ізделінді 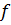 функциясы бар болса, онда әрбір аргумент бойынша сызықтық жайлы (А) қасиетінен мына өрнекті аламыз:
функциясы бар болса, онда әрбір аргумент бойынша сызықтық жайлы (А) қасиетінен мына өрнекті аламыз:
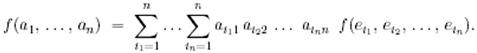
(В) шарты бойынша, кез келген сызықты тәуелді векторлар жүйесінде  болады.
болады.  векторлар жүйесі сонда тек сонда ғана, сызықты тәуелді болады, егер осы векторлардың арасында бірдейі болса (егер бұл векторлардың барлығы қос-қостан әр түрлі болса, онда олар бірлік матрицаның бағандарының ауыстыруын құрайды). Бұдан, қосындыдан нөлдерді алып тастасақ, мына аламыз:
векторлар жүйесі сонда тек сонда ғана, сызықты тәуелді болады, егер осы векторлардың арасында бірдейі болса (егер бұл векторлардың барлығы қос-қостан әр түрлі болса, онда олар бірлік матрицаның бағандарының ауыстыруын құрайды). Бұдан, қосындыдан нөлдерді алып тастасақ, мына аламыз:
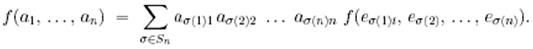
Сонда (А) және (В) шарттарынан 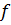 кез келген екі аргументтің орнын ауыстырғанда таңбасы өзгертіндігі шығады.
кез келген екі аргументтің орнын ауыстырғанда таңбасы өзгертіндігі шығады.
Тұжырым. Егер сызықтық тәуелділік индикаторы болатын функция бар болса, онда ол
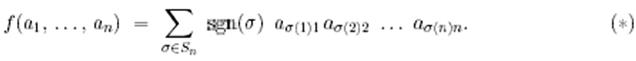
формуласымен анықталады, мұндағы 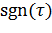 - ауыстыру таңбасы.
- ауыстыру таңбасы.
Теорема (Сызықтық тәуелділік индикаторының бар болуы). Сызықтық тәуелділік индикаторы ((А), (В), (С) шарттарын қанағаттандыратын функция) бар болады, жалғыз және анықтауыш болып табылады.
Тұжырым. Диагональды матрицаның анықтауышы оның диагональдарының элементтерінің көбейтіндісіне тең:
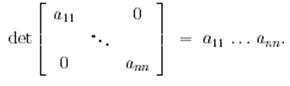
ДӘРІС 7,8
БЛОКТЫ-ҮШБҰРЫШТЫ МАТРИЦА АНЫҚТАУЫШЫ
