Использование F-cтатистики

Однако оценка параметров конкретного уравнения является лишь отдельным эта­пом длительного и сложного процесса построения эконометрической модели. Первое же оцененное уравнение очень редко является удовлетворительным во всех отношениях. Обычно приходится пос­тепенно подбирать формулу связи и состав объясняющих перемен­ных, анализируя на каждом этапе качество оцененной зависимости. Этот анализ качества включает статистическую и содержательную составляющую. Проверка статистического качества оцененного урав­нения состоит из следующих элементов:

• проверка статистической значимости каждого коэффициента урав­нения регрессии;

• проверка общего качества уравнения регрессии;

• проверка свойств данных, выполнение которых предполагалось

при оценивании уравнения.

Под содержательной составляющей анализа качества понимается рассмотрение экономического смысла оцененного уравнения рег­рессии: действительно ли значимыми оказались объясняющие фак­торы, важные с точки зрения теории; положительны или отрица­тельны коэффициенты, показывающие направление воздействия этих факторов; попали ли оценки коэффициентов регрессии в пред­полагаемые из теоретических соображений интервалы. Рассмотрим оценку общего качества уравнения.

Если существует статистически значимая линейная связь вели­чин х и у, то коэффициент R² близок к единице. Однако он может быть близким к единице просто в силу того, что обе эти величины имеют выраженный временной тренд, не связанный с их причин­но-следственной взаимозависимостью. Точную границу приемлемости показателя R² указать сразу для всех случаев невозможно. Нужно принимать во внимание и число степеней свободы уравнения, и наличие трендов переменных, и со­держательную интерпретацию уравнения. Для определения статистической значимости коэффициента де­терминации R² проверяется нулевая гипотеза для F-статистики, рас­считываемой по формуле:

F= 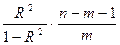, где m - число объясняющих переменных, n- число наблюдений.

Смысл проверяемой гипотезы заключается в том, что все коэффициенты ли­нейной регрессии, за исключением свободного члена, равны нулю. Если они действительно равны нулю для генеральной совокупнос­ти, то уравнение регрессии должно иметь вид 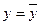, а коэффициент детерминации R² и F-статистика Фишера также равны нулю. При этом их оценки для случайной выборки, конечно, отличаются от нуля, но чем больше такое отличие, тем менее оно вероятно. Логика проверки нулевой гипотезы заключается в том, что если произошло событие, которое было бы слишком маловероятным в том случае, если данная гипотеза действительно была бы верна, то эта гипотеза отвергается.

Величина F, если предположить, что выполнены предпосылки относительно отклонений е_i, имеет распределение Фишера с (т; п-т-1) степенями свободы.

Если F > F(a, n₁, n₂ ), то гипотеза о равенстве нулю всех коэффициентов линейной регрессии отвергается.

Форма проведения: Решение данных задач студентами самостоятельно на местах и при необходимости у доски.

Тема № 9Изучение взаимосвязей непараметрическими методами

Задача 1

Найти выборочный коэффициент ранговой корреляции Спримена по данным ранга объектов выборки объема n = 10:

х
у

Методические рекомендации:

1. Найти разности рангов, возвести их в квадрат.

2. Определить искомый коэффициент ранговой корреляции Спирмена

Задача 2

При уровне значимости 0,05 проверить, является ли ранговая корреляционная связь, вычисленная в задаче1 , значимой.

Методические рекомендации:

1. Найти критическую точку двусторонней области распределения Стьюдента при α=0,05 и степенями свободы n-2.

2. Вычислить критическую точку и сравнить с коэффициентом ранговой корреляции.

Задача 3

Найти выборочный коэффициент ранговой корреляции Кендалла по данным ранга объектов выборки объема n = 10:

х
у

Методические рекомендации:

1. Найти сумму рангов.

2. Определить искомый коэффициент ранговой корреляции Кендалла

Задача 4

При уровне значимости 0,05 проверить, является ли ранговая корреляционная связь, вычисленная в задаче 3 , значимой.

Методические рекомендации:

1. Найти критическую точку по таблице функции Лапласа.

2. Вычислить критическую точку и сравнить с коэффициентом ранговой корреляции Кендалла.

Форма проведения: Решение данных задач студентами самостоятельно на местах и при необходимости у доски.

Основная литература: [5, С.281-343], [7, С.73-114], [11, С.34-54.], [12,С.65-79],[13] [14]

Дополнительная литература: [20] [32]