Мысалды қарастырайық.

Бірінші заводта әр 100 электр шамынан орта мәнімен алғанда 90 –стандартты, екіншісінен -95, үшіншісінен - 85 өндіріледі. Сәйкесінше берілген ауданның дүкеніне түсетін барлық электршамнан 50, 30 және 20% заводтың өнімін құрайды. Стандартты электршамының сатып алуға болатынының ықтималдығын табыңыз.

Шешуі:

Ізделінді оқиғаны A деп, ал бірінші, екінші және үшінші заводтарда шығарылған электршамының оқиғасын сәйкесінше 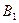, , 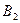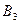деп белгілейік. Шарт бойынша мына оқиғалардың ықтималдығы белгілі: 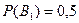, , 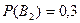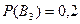және олардың әрқайсысына қатысты А оқиғасының шартты ықтималдығы:

, , .

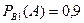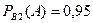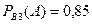Бұл бірінші, екінші және үшінші заводтарда дайындалған стандартты электршамын сатып алу ықтималдығы.

A ізделінді оқиғасы,егер K оқиғасы – электршам бірінші заводта шығарылған және стандартты ( яғни В₁ және A), немесе L оқиғасы – электршам екінші заводта шығарылған және стандартты (яғни В₂ және A), M оқиғасы – электршам үшінші заводта шығарылған және стандартты (яғни В₃ және A).

Ықтималдықтарды қосу теоремасын пайдаланып, мынаны шығарамыз:

.

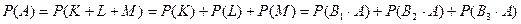Ықтималдықтарды көбейту теоремасын пайдаланып, мынаны шығарамыз:

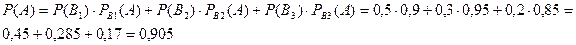
Қорытынды формула – толық ықтималдық формуласының дербес жағдайы болып табылады.

Теорема. Толық тобын құрайтын 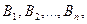үйлесімсіз оқиғалардың біреуі көрінеді деген шартпен пайда болатын А оқиғасының ықтималдығы оның шартына сәйкес келетін осы оқиғалардың әрқайсысының ықтималдықтарының көбейтінділерінің қосындысына тең:

.

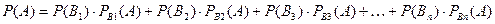Бейес формуласы.

Берілген ауданның дүкеніне түсетін электршамының сапасы және саны алдындағы мысалда келтірілген шарттан анықталады. Электршамдардың шығару орнын және олардың ықтималдықтарын есептейтін мүмкін болжамдарды көрсетіңіз.

Стандартты болып шыққан электршам бірінші, екінші, үшінші заводтарда шығарылуы мүмкін.

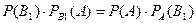, осыдан

,

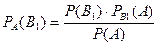мұндағы 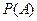- толық ықтималдық формуласы.

Онда

.

.

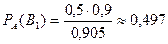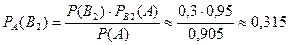
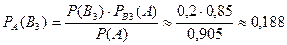Бейес формуласы:

.

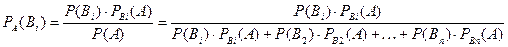Дәріс №3.

Тақырыбы: «Тәуелсіз тәжірибелер. Бернулли формуласы.»

«Лапластың локальдық және интегралдық теоремасы».

Бернулли формуласына әкелетін есепті қарастырайық.

Кездейсоқ алынған 5 бөлшектердің екеуі стандартты болатындығының ықтималдығын тап, егер әр бөлшектің стандартты болатынының ықтималдығы 0,9-ға тең болса.

Шешуі:

Кездейсоқ алынған шар стандартты деп болжамдап алынған А оқиғасының ықтималдығы 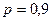, оның стандартты емес екендігінің ықтималдығы 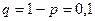. Ізделінді оқиға (оны В арқылы белгілейміз), егер алғашқы екі бөлшек стандартты, ал қалған үшеуі стандартты емес болса болады. В оқиғасы сонымен қатар, егер 1-ші және 3-ші бөлшектер стандартты, ал қалғаны стандартты емес болса да болады. В оқиғасының болуының басқа да мүмкіндіктері бар. Олардың бәрі де кездейсоқ алынған бесеуінің қандай да бір орын алатын екеуі стандартты болуымен сипатталады. Сондықтан, В оқиғасының орындалу мүмкіндіктерінің жалпы саны бесеуінен екеуі үйлесімді болғандағы санына тең, яғни: .

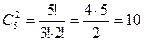Ықтималдықтарды көбейту теоремасы бойынша әр мүмкіндіктің ықтималдығы бес көбейткіштің көбейтіндісіне тең, олардың екеуінің стандартты болатыны 0,9-ға, стандартты емес болатыны 0,1-ге тең, яғни 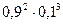ықтималдығын құрайды. Көрсетілген 10 мүмкіндіктер үйлесімсіз оқиға болғандықтан, 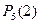деп белгіленген В оқиғасының ықтималдықтарын қосу теоремасы бойынша мынаған тең:

.

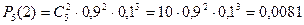Есептің шешімінің қорытындысын осылай түрлендіруге болады:

Әр тәжірибеде А оқиғасы болатындығының р ықтималдығы тұрақты болса, n тәуелсіз тәжірибелерінде А оқиғасы дәл k рет болатынның 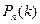ықтималдығы мына формула бойынша есептеледі: 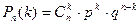, Мұндағы .

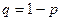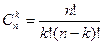ауыстырып, мынаны шығарамыз:

.

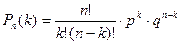Мысал .

Тиын 8 рет лақтырылды. Оның 6 рет жалау жағымен төменге қарап түсетінінің ықтималдығы қандай?

Шешуі:

n=8, k=6, p=0,5, q=0,5

.

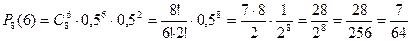Егер тәжірибелер саны үлкен болса, ал тәжірибеде оқиғаның көріну ықтималдығы өте аз болса, онда жуық формуласын қолданады:

P_n(k)= ,

Мұндағы

,

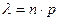k – 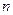тәуелсіз тәжірибелерде оқиғаның көріну саны. Берілген жағдайда кездейсоқ шама Пуассон заңы бойынша үлестірілген делінеді.