В частных производных второго порядка

Линейные относительно вторых производных уравнения

(21)

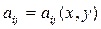где и 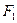произвольная функция пяти переменных, относятся к одному из трех типов в зависимости от знака дискриминанта

(22)

Если дискриминант D>0, то уравнение (21) называется уравнением ги-

перболического типа; если D<0, то уравнение (21) называется уравнени-

ем эллиптического типа; если дискриминант D=0, то уравнение (21) называется уравнением параболического типа.

По левой части (21) составляется уравнение характеристик

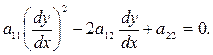(23)

Если D>0, то уравнение (23) распадается на два обыкновенных дифе- ренциальных уравнения первого порядка, и при их решении получим два общих интеграла

(24)

Их левые части нужно брать в качестве новых переменных

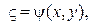относительно которых получим каноническое уравнение

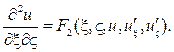(25)

Если D<0, то левые части соотношений (4), будут комплексно-сопряженными и в качестве новых переменных выбирают

Соответственно придем к каноническому уравнению эллиптического типа

(26)

В параболическом случае, когда D=0, уравнение характеристик сводится к одному уравнению, соответственно получится один общий интеграл

(24^/)

Вводятся новые переменные 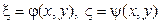, где в качестве второй переменной берется любая функция 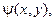функционально независимая от 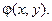В итоге придем к каноническому параболическому уравнению

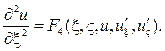(27)

Будем рассматривать линейные уравнения в частных производных

2-го порядка

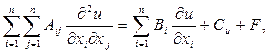(28)

где 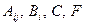суть функции от независимых переменных

На этот раз тип уравнения (28) можно определить только для фиксированной точки

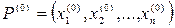
по левой части уравнения, точнее по коэффициентам

путем введения новых переменных

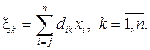(29)

Относительно новых переменных придем к уравнению

(28^/)

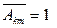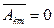Говорят, что уравнение (28) имеет в данной точке Р⁽⁰⁾ эллиптичес- кий тип, если существует невырожденное преобразование вида (29) та- кое, что в уравнении (28^/) при , при

Говорят, что уравнение (28) имеет в данной точке Р⁽⁰⁾ гиперболичес- кий тип, если существует невырожденное преобразование вида (29) та- кое, что в уравнении (28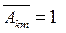^/) при 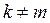а среди коэффициентов имеется v коэффициентов, равных единице, и n-v коэффициентов, равных минус-единице.

Говорят, что уравнение (28) имеет в данной точке Р⁽⁰⁾ параболический тип, если существует невырожденное преобразование вида (29) такое, что в уравнении (28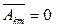^/) при 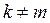, а среди коэффициентов 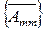наряду с единицами и минус-единицами также имеются нули.

Если в уравнении (28) коэффициенты левой части A_ij постоянные, то из приведенных определений ясно, что это уравнение будет иметь один и тот же тип во всем n-мерном пространстве.

122. Приведите к каноническому виду уравнение

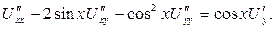
Р е ш е н и е. Дискриминант 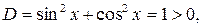т. е. уравнение имеет гиперболический тип. Уравнение характеристик

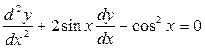
распадается на два уравнения

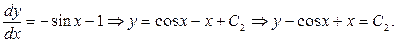
Вводим новые переменные 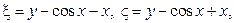тогда

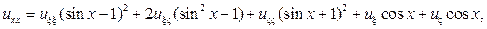
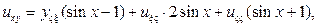
Подставляя найденные производные в исходное уравнение, получим

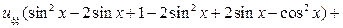
123. Приведите к каноническому виду уравнение

Р е ш е н и е. Дискриминант т.е. уравнение имеет

эллиптический тип. Уравнение характеристик

распадается на два дифференциальных уравнения с комплексно сопряженными правыми частями. Решаем одно из них

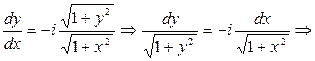
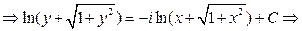
Вводим новые переменные, полагая 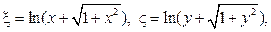тогда

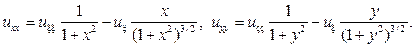
Подставляя найденные производные в исходное уравнение будем иметь

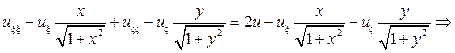
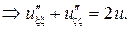
124. Приведите к каноническому виду уравнение

Р е ш е н и е. Дискриминант 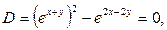т.е. уравнение имеет параболический тип. Уравнение характеристик

имеет один общий интеграл

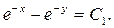
Вводим новые переменные Тогда

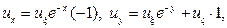
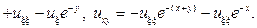
Подставляя найденные производные в исходное уравнение, получим

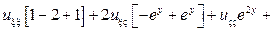
125. Приведите к каноническому виду уравнение

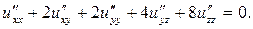(30)

Рассмотрим квадратичную форму

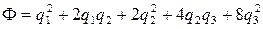
По методу Лагранжа ее можно записать в форме

Полагая 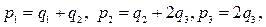получим относительно но- вых переменных квадратичную форму

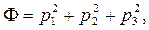
и это означает, что дифференциальное уравнение имеет эллиптический тип и приводится к виду

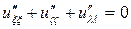(30^/)

с помощью линейной замены. Для ее нахождения выразим переменные 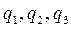через переменные так, что

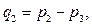
или в матричной форме

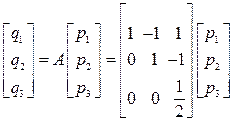
Теперь нужно взять транспонированную матрицу и использовать равенство

,

или в скалярной форме

Определите тип и приведите к каноническому виду следующие уравнения второго порядка:

126.

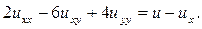
127.

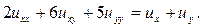
128.

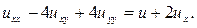
129.

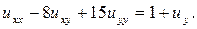
130.

131.

132.

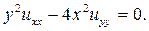
133.

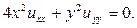
134.

135.

136.

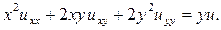
137.

138.

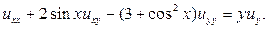
139.

140.

141.

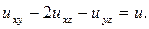
142.

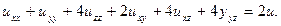
143.

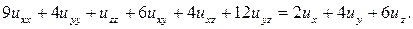
ПРОСТЕЙШИЙ ВАРИАНТ МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ

Рассмотрим смешанную задачу для однородного уравнения колебаний струны:

Будем искать решение в форме

u(x,t) = X(x)T(t). (34)

Подставляя (34) в (31) и разделяя переменные, получим соответст- венно

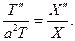
Поскольку это должно быть тождеством, то на самом деле его левая часть не зависит от t, а правая часть не зависит от x, их следует приравнять к некоторой константе так, что имеем

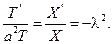(35)

С другой стороны, подставляя (34) в (32), найдем

(36)

Если T(t)=0,то из (34) вытекает u(x,t)=0, а нам нужно искать нетриви- альные решения уравнения (31). Стало быть, T(t)¹0 и из (36) имеем гра -ничные условия для функции Х(х) в виде Х(0)=Х =0. Присоединяя эти граничные условия к дифференциальному уравнению для функции Х(х) , из соотношения (35) получим так называемую задачу Штурма Лиувил- ля

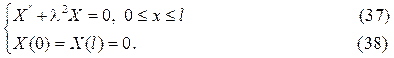
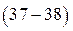Подлежат нахождению функция Х(х) и параметр . Очевидно, что при любых задача имеет тривиальное решение Х(х)º0, но есть еще и нетривиальные решения по крайней мере при некоторых .

Определение. Те значения параметра , при которых задача 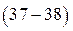имеет нетривиальные решения, называются собственными значениями, а соответствующие нетривиальные решения называются собственными функциями.

С учетом названного определения говорят, что решить задачу Штур- ма Лиувилля 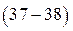– значит найти ее собственные значения и соб- ственные функции.

Общее решение уравнения (37) как линейного уравнения с постоянны- ми коэффициентами запишется в виде

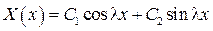
Добиваясь выполнения граничных условий (38), имеем

С₁ × 1 + С₂ × 0 = 0 Þ С₁=0.

Если С₂=0, то придем к тривиальному решению Х(х)º0, поэтому С₂¹0 и пусть для определенности С₂=1. Из второго граничного условия выте -кает, что sinl 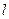=0 и, следовательно 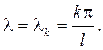Соответствующие собст -венные функции примут вид

(39)

Теперь возвращаемся к равенству (35) и берем дифференциальное уравнение для функции Т(t) при :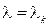

Его общее решение будет иметь вид

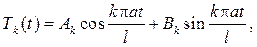
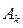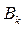где и – произвольные постоянные.

Согласно (34) произведения собственных функций (39) на соответству- ющие решения

будут решать задачу (31 32) при любых 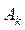и 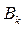. Ввиду однородности уравнения и граничных условий сумма конечного числа этих произведе -ний также будет решением задачи (31-32).

Более того, ряд

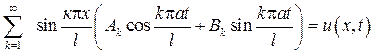(40)

если только он допускает двойное почленное дифференцирование по пе- ременным – x и t, также будет решением задачи (31 32). Остается выбрать коэффициенты и 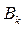такими, чтобы выполнялись начальные условия.

Подставляя (40) в (33), будем иметь

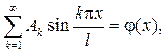
откуда по формулам для коэффициентов Фурье получим

(41)

Из второго граничного условия найдем, что

и, стало быть,

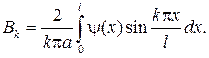(42)

Мы получили, что сумма ряда (40) будет решением исходной задачи (31) 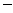(33) , если коэффициенты и 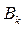определены по формулам (41), (42). При определенных условиях на гладкость граничных функци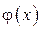й и ряд (40) будет допускать двойное почленное дифференцирова-

ние (см. [1]) , и его сумма будет классическим решением задачи (31) 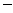(33). В других ситуациях сумму ряда (40) называют обобщенным или формальным решением задачи (31) 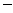(33).

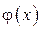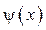Изложенная схема решения смешанной задачи принципиально не ме-няется и при других однородных граничных условий. Считается целесо-образным запоминать метод решения, а не его детали, поэтому при реше- нии примеров с конкретными граничными функциями и вы-

полняются те же самые действия ( или аналогичные при измененных граничных условиях (32)) и в той же последовательности, что и при об- щих начальных условиях (33). Заметим, что такая традиция соблюдается в целом при решении дифференциальных уравнений.

144.Однородная струна, жестко закрепленная в концевых точках x=0 и , имеет в начальный момент времени t=0 форму

Определить смещение u(x,t) точек струны от прямолинейного положе- ния равновесия, предполагая, что начальные скорости отсутствуют.