Выбор формы уравнения регрессии

Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные.

Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессии 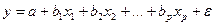параметры при 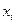называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:

,

где 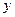– расходы семьи за месяц на продукты питания, тыс. руб.;

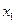– месячный доход на одного члена семьи, тыс. руб.;

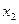– размер семьи, человек.

Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Параметр не подлежит экономической интерпретации.

При изучении вопросов потребления коэффициенты регрессии рассматриваются как характеристики предельной склонности к потреблению. Например, если функция потребления 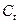имеет вид

,

то потребление в период времени 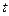зависит от дохода того же периода , и от дохода предшествующего периода 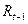. Соответственно коэффициент 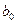характеризует эффект единичного возрастания дохода при неизменном уровне предыдущего дохода. Коэффициент 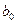обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на 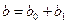. Коэффициент рассматривается здесь как долгосрочная склонность к потреблению. Так как коэффициенты и , то долгосрочная склонность к потреблению должна превосходить краткосрочную 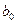. Например, за период 1905-1951 гг. (за исключением военных лет) М.Фридман построил для США следующую функцию потребления: с краткосрочной предельной склонностью к потреблению 0,58 и с долгосрочной склонностью к потреблению 0,9.

Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т. е. от предыдущего уровня потребления :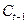

В этом уравнении параметр 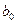также характеризует краткосрочную предельную склонность к потреблению, т. е. влияние на потребление единичного роста доходов того же периода . Долгосрочную предельную склонность к потреблению здесь измеряет выражение .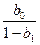

Так, если уравнение регрессии составило

,

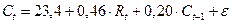то краткосрочная склонность к потреблению равна 0,46, а долгосрочная –0,575 (0,46/0,8).

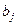В степенной функции коэффициенты являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

В производственных функциях вида

,

где 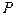– количество продукта, изготавливаемого с помощью от производственных факторов ( );

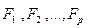– параметр, являющийся эластичностью количества продукции по отношению к количеству соответствующих производственных факторов,

экономический смысл имеют не только коэффициенты 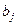каждого фактора, но и их сумма, т.е. сумма эластичностей: 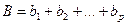. Эта величина фиксирует обобщенную характеристику эластичности производства. Пусть производственная функция имеет вид

,

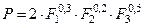где 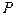– выпуск продукции;

– стоимость основных производственных фондов;

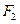– отработано человеко-дней;

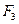– затраты на производство,

Эластичность выпуска по отдельным факторам производства составляет в среднем 0,3 % с ростом на 1 % при неизменном уровне других факторов; 0,2 % – с ростом 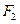на 1 % также при неизменности других факторов производства и 0,5 % с ростом 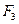на 1 % при неизменном уровне других факторов. Для данного уравнения 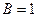. Следовательно, в целом с ростом каждого фактора производства на 1% коэффициент эластичности выпуска продукции составляет 1%, т.е. выпуск продукции увеличивается на 1%, что в микроэкономике соответствует постоянной отдаче на масштаб.

При практических расчетах не всегда 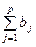. Она может быть как больше, так и меньше единицы. В этом случае величина фиксирует приближенную оценку эластичности выпуска с ростом каждого фактора производства на 1 % в условиях увеличивающейся (В > 1) или уменьшающейся (В < 1) отдачи на масштаб.

Возможны и другие линеаризуемые функции для построения уравнения множественной регрессии.

Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбрать ту из них, для которой остаточная дисперсия и ошибка аппроксимации минимальны, а коэффициент детерминации максимален.

Если исследователя не устраивает предлагаемый стандартной программой набор функций регрессии, то можно использовать любые другие функции, приводимые путем соответствующих преобразований к линейному виду. Однако чем сложнее функция, тем менее интерпретируемы ее параметры.

При сложных полиномиальных функциях с большим числом факторов необходимо помнить, что каждый параметр преобразованной функции является средней величиной, которая должна быть подсчитана по достаточному числу наблюдений. Если число наблюдений невелико, что, как правило, имеет место в эконометрике, то увеличение числа параметров функции приведет к их статистической незначимости и соответственно потребует упрощения вида функции. Если один и тот же фактор вводится в регрессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Так, если модель имеет вид полинома второго порядка

,

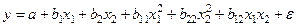то после замены переменных 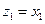, , 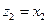, , 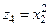получим линейное уравнение регрессии с пятью факторами:

.

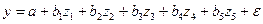Поскольку, как отмечалось, должно выполняться соотношение между числом параметров и числом наблюдений, для полинома второй степени требуется не менее 30–35 наблюдений.

В эконометрике регрессионные модели часто строятся на основе макроуровня экономических показателей, когда ставится задача оценки влияния наиболее экономически существенных факторов на моделируемый показатель при ограниченном объеме информации. Поэтому полиномиальные модели высоких порядков используются редко.