Внецентренное сжатие или растяжение.
Вторым практически важным случаем сложения деформаций от изгиба и от продольных сил является так называемое внецентренное сжатие или растяжение, вызываемое одними продольными силами. Этот вид деформации получается при действии на стержень двух равных и прямопротивоположных сил Р, направленных по прямой АА, параллельной оси стержня (Рис.3 а). Расстояние точки А от центра тяжести сечения ОА=е называется эксцентриситетом.
Рассмотрим сначала случай внецентренного сжатия, как имеющий большее практическое значение.
Нашей задачей явится нахождение наибольших напряжений, материале стержня и проверка прочности. Для решения этой задачи приложим в точках О по две равные и противоположные силы Р (Рис.3 б). Это не нарушит равновесия стержня в целом и не изменит напряжений в его сечениях.
Силы Р, зачеркнутые один раз, вызовут осевое сжатие, а пары сил Р, зачеркнутые дважды, вызовут чистый изгиб моментами 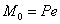 . Расчетная схема стержня показана на Рис.3 в. Так как плоскость действия изгибающих пар ОА может не совпадать ни с одной из главных плоскостей инерции стержня, то в общем случае имеет место комбинация продольного сжатия и чистого косого изгиба.
. Расчетная схема стержня показана на Рис.3 в. Так как плоскость действия изгибающих пар ОА может не совпадать ни с одной из главных плоскостей инерции стержня, то в общем случае имеет место комбинация продольного сжатия и чистого косого изгиба.
Так как при осевом сжатии и чистом изгибе напряжения во всех сечениях одинаковы, то проверку прочности можно произвести для любого сечения, хотя бы С—С (Рис.3 б, в).
Отбросим верхнюю часть стержня и оставим нижнюю (Рис.3 г). Пусть оси Оу и Oz будут главными осями инерции сечения.
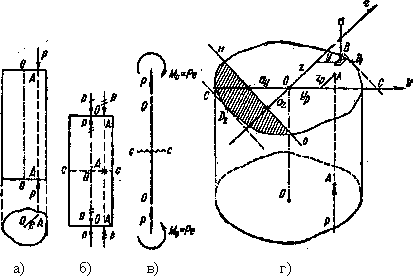
Рис.3. а) расчетная схема б) преобразование нагрузок в)приведенная расчетная схема г) механизм исследования напряжений
Координаты точки А, — точки пересечения линии действия сил Р с плоскостью сечения, — пусть будут 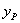 и
и 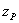 . Условимся выбирать положительные направления осей Оу и Oz таким образом, чтобы точка А оказалась в первом квадранте. Тогда
. Условимся выбирать положительные направления осей Оу и Oz таким образом, чтобы точка А оказалась в первом квадранте. Тогда 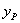 и
и 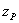 будут положительны.
будут положительны.
Для того чтобы отыскать наиболее опасную точку в выбранном сечении, найдем нормальное напряжение 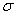 в любой точке В с координатами z и у. Напряжения в сечении С — С будут складываться из напряжений осевого сжатия силой Р и напряжений от чистого косого изгиба парами с моментом Ре, где
в любой точке В с координатами z и у. Напряжения в сечении С — С будут складываться из напряжений осевого сжатия силой Р и напряжений от чистого косого изгиба парами с моментом Ре, где 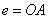 . Сжимающие напряжения от осевых сил Р в любой точке равны
. Сжимающие напряжения от осевых сил Р в любой точке равны 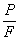 , где
, где 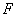 — площадь поперечного сечения стержня; что касается косого изгиба, то заменим его действием изгибающих моментов в главных плоскостях. Изгиб в плоскости х Оу вокруг нейтральной оси Oz будет вызываться моментом
— площадь поперечного сечения стержня; что касается косого изгиба, то заменим его действием изгибающих моментов в главных плоскостях. Изгиб в плоскости х Оу вокруг нейтральной оси Oz будет вызываться моментом 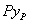 и даст в точке В нормальное сжимающее напряжение
и даст в точке В нормальное сжимающее напряжение
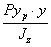
Точно так же нормальное напряжение в точке В от изгиба в главной плоскости х Oz, вызванное моментом 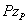 , будет сжимающим и выразится формулой
, будет сжимающим и выразится формулой 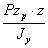 .
.
Суммируя напряжения от осевого сжатия и двух плоских изгибов и считая сжимающие напряжения отрицательными, получаем такую формулу для напряжения в точке В:
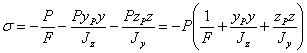 | (1) |
Эта формула годится для вычисления напряжений в любой точке любого сечения стержня, стоит только вместо у и z подставить координаты точки относительно главных осей с их знаками.
В случае внецентренного растяжения знаки всех составляющих нормального напряжения в точке В изменятся на обратные. Поэтому для того, чтобы получать правильный знак напряжений как при внецентренном сжатии, так и при внецентренном растяжении, нужно, кроме знаков координат у и z, учитывать также и знак силы Р; при растяжении перед выражением
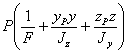
должен стоять знак плюс, при сжатии — минус.
Полученной формуле можно придать несколько иной вид; вынесем за скобку множитель 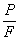 ; получим:
; получим:
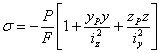 | (2) |
Здесь 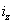 и
и 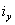 — радиусы инерции сечения относительно главных осей (вспомним, что
— радиусы инерции сечения относительно главных осей (вспомним, что 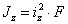 и
и 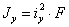 ).
).
Для отыскания точек с наибольшими напряжениями следует так выбирать у и z, чтобы 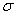 достигло наибольшей величины. Переменными в формулах (1) и (2) являются два последних слагаемых, отражающих влияние изгиба. А так как при изгибе наибольшие напряжения получаются в точках, наиболее удаленных от нейтральной оси, то здесь, как и при косом изгибе, надо отыскать положение нейтральной оси.
достигло наибольшей величины. Переменными в формулах (1) и (2) являются два последних слагаемых, отражающих влияние изгиба. А так как при изгибе наибольшие напряжения получаются в точках, наиболее удаленных от нейтральной оси, то здесь, как и при косом изгибе, надо отыскать положение нейтральной оси.
Обозначим координаты точек этой линии через 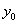 и
и 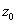 ; так как в точках нейтральной оси нормальные напряжения равны нулю, то после подстановки в формулу (2) значений
; так как в точках нейтральной оси нормальные напряжения равны нулю, то после подстановки в формулу (2) значений 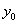 и
и 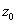 получаем:
получаем:
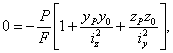
или
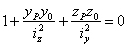 | (3) |
Это и будет уравнение нейтральной оси. Очевидно, мы получили уравнение прямой, не проходящей через центр тяжести сечения.
Чтобы построить эту прямую, проще всего вычислить отрезки, отсекаемые ею на осях координат. Обозначим эти отрезки 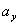 и
и 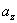 . Чтобы найти отрезок
. Чтобы найти отрезок 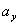 , отсекаемый на оси Оу, надо в уравнении (3) положить
, отсекаемый на оси Оу, надо в уравнении (3) положить
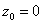 ;
; 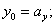
тогда мы получаем:
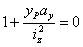 и и 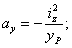 | (4) |
подобным же образом, полагая
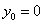 ;
; 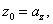
получаем:
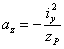 | (5) |
Если величины 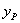 и
и 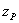 положительны, то отрезки
положительны, то отрезки 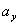 и
и 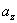 будут отрицательны, т. е. нейтральная ось будет расположена по другую сторону центра тяжести сечения, чем точка А (Рис.3 г).
будут отрицательны, т. е. нейтральная ось будет расположена по другую сторону центра тяжести сечения, чем точка А (Рис.3 г).
Нейтральная ось делит сечение на две части — сжатую и растянутую; на Рис.3 г растянутая часть сечения заштрихована. Проводя к контуру сечения касательные, параллельные нейтральной оси, получаем две точки 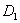 и
и 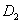 , в которых будут наибольшие сжимающие и растягивающие напряжения.
, в которых будут наибольшие сжимающие и растягивающие напряжения.
Измеряя координаты у и z этих точек и подставляя их значения в формулу (1), вычисляем величины наибольших напряжений в точках 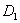 и
и 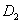 :
:
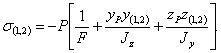
Если материал стержня одинаково сопротивляется растяжению и сжатию, то условие прочности получает такой вид:
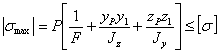
Для поперечных сечений с выступающими углами, у которых обе главные оси инерции являются осями симметрии (прямоугольник, двутавр и др.) 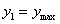 и
и 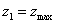 Поэтому формула упрощается, и мы имеем
Поэтому формула упрощается, и мы имеем
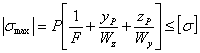
Если же материал стержня неодинаково сопротивляется растяжению и сжатию, то необходимо проверить прочность стержня как в растянутой, так и в сжатой зонах.
Однако может случиться, что и для таких материалов будет достаточно одной проверки прочности. Из формул (4) и (5) видно, что положение точки А приложения силы и положение нейтральной оси связаны: чем ближе подходит точка А к центру сечения, тем меньше величины 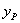 и
и 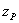 и тем больше отрезки
и тем больше отрезки 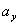 и
и 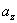 . Таким образом, с приближением точки А к центру тяжести сечения нейтральная ось удаляется от него, и наоборот. Поэтому при некоторых положениях точки А нейтральная ось будет проходить вне сечения и все сечение будет работать на напряжения одного знака. Очевидно в этом случае всегда достаточно проверить прочность материала в точке
. Таким образом, с приближением точки А к центру тяжести сечения нейтральная ось удаляется от него, и наоборот. Поэтому при некоторых положениях точки А нейтральная ось будет проходить вне сечения и все сечение будет работать на напряжения одного знака. Очевидно в этом случае всегда достаточно проверить прочность материала в точке 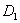 .
.
Разберем практически.важный случай, когда к стержню прямоугольного сечения (Рис. 4) приложена внецентренно сила Р в точке А, лежащей на главной оси сечения Оу. Эксцентриситет ОА равен е, размеры сечения b и d. Применяя полученные выше формулы, имеем:
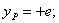
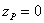
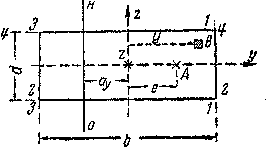
Рис.4. Расчетная схема бруса прямоугольного сечения.
Напряжение в любой точке В равно
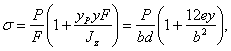
так как
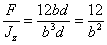
Напряжения во всех точках линии, параллельной оси Oz, одинаковы. Положение нейтральной оси определяется отрезками
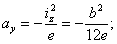
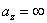
Нейтральная ось параллельна оси Oz; точки с наибольшими растягивающими и сжимающими напряжениями расположены на сторонах 1—1 и 3—3.
Значения 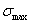 и
и  получатся, если подставить вместо у его значения
получатся, если подставить вместо у его значения 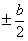 . Тогда
. Тогда
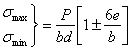
Лекция № 28. Ядро сечения при внецентренном сжатии
При конструировании стержней из материалов, плохо сопротивляющихся растяжению (бетон), весьма желательно добиться того, чтобы все сечение работало лишь на сжатие. Этого можно достигнуть, не давая точке приложения силы Р слишком далеко отходить от центра тяжести сечения, ограничивая величину эксцентриситета.
Конструктору желательно заранее знать, какой эксцентриситет при выбранном типе сечения можно допустить, не рискуя вызвать в сечениях стержня напряжений разных знаков. Здесь вводится понятие о так называемом ядре сечения. Этим термином обозначается некоторая область вокруг центра тяжести сечения, внутри которой можно располагать точку приложения силы Р, не вызывая в сечении напряжений разного знака.
Пока точка А располагается внутри ядра, нейтральная ось не пересекает контура сечения, все оно лежит по одну сторону от нейтральной оси и, стало быть, работает лишь на сжатие. При удалении точки А от центра тяжести сечения нейтральная ось будет приближаться к контуру; граница ядра определится тем, что при расположении точки А на этой границе нейтральная ось подойдет вплотную к сечению, коснется его.
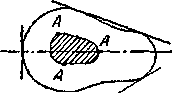
Рис.1. Комбинации положения сжимающей силы и нейтральной линии
Таким образом, если мы будем перемещать точку А так, чтобы нейтральная ось катилась по контуру сечения, не пересекая его, то точка А обойдет по границе ядра сечения. Если контур сечения имеет «впадины», то нейтральная ось будет катиться по огибающей контура.
Чтобы получить очертание ядра, необходимо дать нейтральной оси несколько положений, касательных к контуру сечения, определить для этих положений отрезки 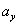 и
и 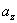 и вычислить координаты
и вычислить координаты 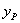 и
и 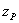 точки приложения силы по формулам, вытекающим из известных зависимостей:
точки приложения силы по формулам, вытекающим из известных зависимостей:
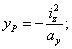
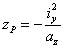
это и будут координаты точек контура ядра 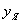 и
и 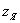 .
.
При многоугольной форме контура сечения (Рис.2), совмещая последовательно нейтральную ось с каждой из сторон многоугольника, мы по отрезкам 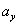 и
и 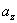 определим координаты
определим координаты 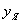 и
и 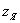 точек границы ядра, соответствующих этим сторонам.
точек границы ядра, соответствующих этим сторонам.
При переходе от одной стороны контура сечения к другой нейтральная ось будет вращаться вокруг вершины, разделяющей эти стороны; точка приложения силы будет перемещаться по границе ядра между полученными уже точками. Установим, как должна перемещаться сила Р, чтобы нейтральная ось проходила все время через одну и ту же точку В ( 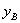 ,
, 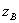 ) — вращалась бы около нее. Подставляя координаты этой точки нейтральной оси в известное уравнение нейтральной оси (линии), получим:
) — вращалась бы около нее. Подставляя координаты этой точки нейтральной оси в известное уравнение нейтральной оси (линии), получим:
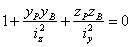
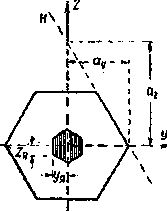
Рис.2. Ядро сечения для многоугольной формы поперечного сечения
Таким образом координаты 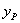 и
и 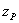 точки
точки 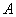 приложения силы Р связаны линейно. При вращении нейтральной оси около постоянной точки В точка А приложения силы движется по прямой. Обратно, перемещение силы Р по прямой связано с вращением нейтральной оси около постоянной точки.
приложения силы Р связаны линейно. При вращении нейтральной оси около постоянной точки В точка А приложения силы движется по прямой. Обратно, перемещение силы Р по прямой связано с вращением нейтральной оси около постоянной точки.
На Рис.3 изображены три положения точки приложения силы на этой прямой и соответственно три положения нейтральной оси. Таким образом, при многоугольной форме контура сечения очертание ядра между точками, соответствующими сторонам многоугольника, будет состоять из отрезков прямых линий.
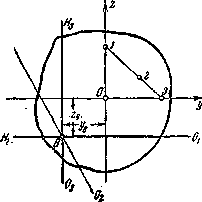
Рис.3. Динамика построения ядра сечения
Если контур сечения целиком или частично ограничен кривыми линиями, то построение границы ядра можно вести по точкам. Рассмотрим несколько простых примеров построения ядра сечения.
При выполнении этого построения для прямоугольного поперечного сечения воспользуемся полученными формулами.
Для определения границ ядра сечения при движении точки А по оси Оу найдем то значение 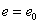 , при котором нейтральная ось займет положение Н1О1. Имеем:
, при котором нейтральная ось займет положение Н1О1. Имеем:
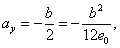
откуда
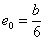
Таким образом, границы ядра по оси Оу будут отстоять от центра сечения на 1/6 величины b (Рис.4, точки 1 и 3); по оси Oz границы ядра определятся расстояниями 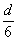 (точки 2 и 4).
(точки 2 и 4).
Для получения очертания ядра целиком изобразим положения нейтральной оси 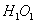 и
и 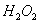 , соответствующие граничным точкам 1 и 2.
, соответствующие граничным точкам 1 и 2.
При перемещении силы из точки 1 в точку 2 по границе ядра нейтральная ось должна перейти из положения 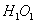 в положение
в положение 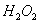 , все время касаясь сечения, т. е. поворачиваясь вокруг точки D.
, все время касаясь сечения, т. е. поворачиваясь вокруг точки D.
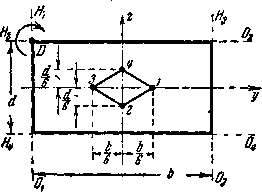
Рис.4. построение ядра для прямоугольного сечения.
Для этого сила должна двигаться по прямой 1 — 2. Точно так же можно доказать, что остальными границами ядра будут линии 2—3, 3—4 и 4—1.
Таким образом, для прямоугольного сечения ядро будет ромбом с диагоналями, равными одной трети соответствующей стороны сечения. Поэтому прямоугольное сечение при расположении силы по главной оси работает на напряжения одного знака, если точка приложения силы не выходит за пределы средней трети стороны сечения.
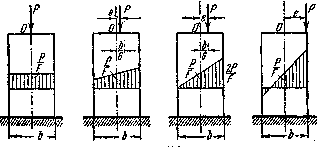
Рис.5. Динамика изменения напряжений при изменении эксцентриситета.
Эпюры распределения нормальных напряжений по прямоугольному сечению при эксцентриситете, равном нулю, меньшем, равном и большем одной шестой ширины сечения, изображены на Рис.5.
Отметим, что при всех положениях силы Р напряжение в центре тяжести сечения (точка О) одинаково и равно 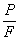 и что сила Р не имеет эксцентриситета по второй главной оси.
и что сила Р не имеет эксцентриситета по второй главной оси.
Для круглого сечения радиуса r очертание ядра будет по симметрии кругом радиуса 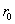 . Возьмем какое-либо положение нейтральной оси, касательное к контуру. Ось Оу расположим перпендикулярно к этой касательной. Тогда
. Возьмем какое-либо положение нейтральной оси, касательное к контуру. Ось Оу расположим перпендикулярно к этой касательной. Тогда
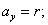
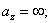
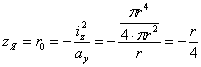
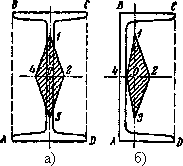
Рис.6. Ядро сечения для двутавра — а) и швеллера — б)
Таким образом, ядро представляет собой круг с радиусом, вчетверо меньшим, чем радиус сечения.
Для двутавра нейтральная ось при обходе контура не будет пересекать площади поперечного сечения, если будет касаться прямоугольного контура ABCD, описанного около двутавра (Рис.6а). Следовательно, очертание ядра для двутавра имеет форму ромба, как и для прямоугольника, но с другими размерами.
Для швеллера, как и для двутавра, точки 1, 2, 3, 4 контура ядра (Рис.6 б) соответствуют совпадению нейтральной оси со сторонами прямоугольника ABCD.
Лекция № 29. Совместные действия изгиба и кручения призматического стержня
Исследуем этот вид деформации стержня на примере расчета вала кругового (кольцевого) поперечного сечения на совместное действие изгиба и кручения (рис. 1).

Рис.1. Расчетная схема изогнутого и скрученного вала
