П.1 Восстановление оригиналов с помощью таблиц.

Этот способ является самым простым, но удобен в применении только, если изображение легко сводится к табличному виду элементарными преобразованиями.

Пример1. Найти оригинал изображения .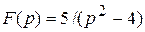

Решение.

Приведем 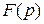к табличному виду

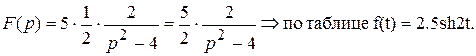
Пример 2. Найти оригинал изображения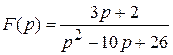

Решение.

Приведем 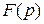к табличному виду

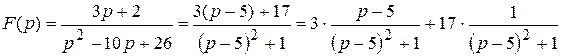
По таблице получаем, что .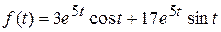

Пример 3. Найти оригинал изображения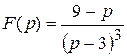

Решение. Приведем 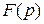к табличному виду: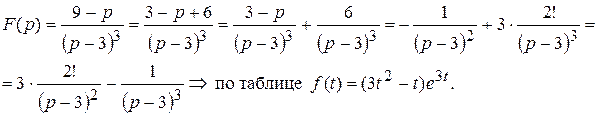

Примеры для самостоятельного решения.

Найти оригинал изображения.

1)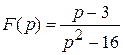;	3);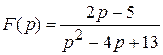
2)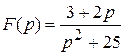;	4).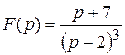

Ответы :

1) 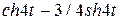;	3) ;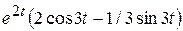
2) 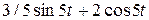;	4) .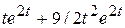

П.2 Восстановление оригиналов с помощью свертки.

Этот вопрос подробно был рассмотрен в § 9, поэтому сразу перейдем к примерам.

Пример 1. Восстановить оригинал следующего изображения : .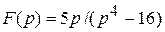

Решение.

Преобразуем изображение к виду удобному для применения теоремы о свертке.

.

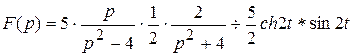По таблице сверток находим, что оригинал для этого изображения имеет вид :

.

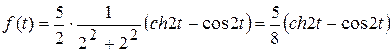Пример 2. Восстановить оригинал следующего изображения : .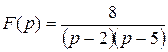

Решение.

Преобразуем изображение к виду удобному для применения теоремы о свертке:

.

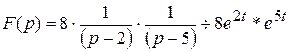По таблице сверток находим, что оригинал для этого изображения имеет вид: .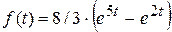

Примеры для самостоятельного решения можно взять из §7.

П.3 Нахождение оригиналов с помощью разложения дроби на сумму простейших.

Если изображение является правильной дробью, то методом неопределенных коэффициентов эту дробь можно представить в виде суммы простейших дробей I-IV типов так, как это делалось при интегрировании рациональных дробей. При этом дробь 1-го типа 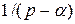соответствуют оригиналу 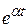, дробь 2-го типа 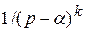соответствует оригиналу 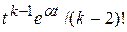, дробь 3-го типа сначала преобразовывается к виду:

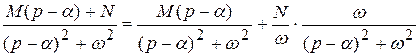, а затем по таблице определяется оригинал: .

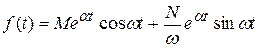Выполнив аналогичные преобразования для дробей 4-го типа, можно найти для них оригиналы или по таблицам, или с помощью свертки.

Пример 1. Найти оригинал следующего изображения: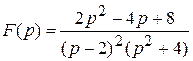

Решение.

Представим эту дробь в виде суммы простейших дробей:

.

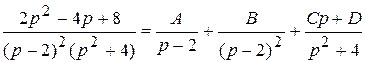Найдем A , B, C, D методом неопределенных коэффициентов.

2p²-4p+8=A(p-2)(p²+4)+B(p²+4)+(p-2)²(Cp+D)

При

p=2 8=8B , т.е. B=1

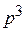: 0=A+C

: 2=-2A+B+D-4C

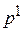: -4=4A+4C-4D D=1(A+C=0)

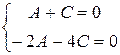A=0, C=0

Получили, что F(p)= 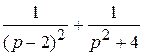. Применяя теоремы линейности и затухания, находим оригинал: .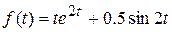

Пример 2.

Найти оригинал следующего изображения: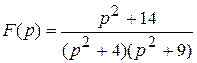

Решение.

Представим 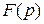в виде суммы простейших дробей:

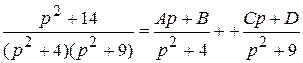,т.е.

.

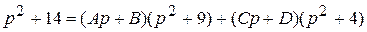Приравниваем коэффициенты при равных степенях:

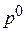: 14=9B+4D

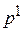: 0=9A+4C

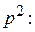1=B+D

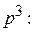0=A+C. Решая соответствующие системы, получаем, что

A=0; C=0; B=2; D=-1 .

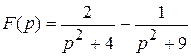,т.е. .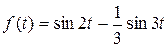

При решении этих задач использовались теоремы единственности, линейности, затухания, таблица оригиналов и изображений.

Примеры для самостоятельного решения.

Найти оригинал изображения

1)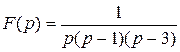 ;	5) ;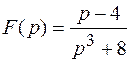
2)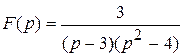 ;	4) ;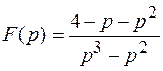
3)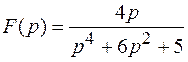 ;	6) .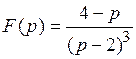

Ответы.